题目内容
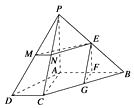
【题目】如图,三棱锥P﹣ABC中,D,E分别是BC,AC的中点.PB=PC=AB=2,AC=4,BC=2 ![]() ,PA=
,PA= ![]() .
. 
(1)求证:平面ABC⊥平面PED;
(2)求AC与平面PBC所成的角;
(3)求平面PED与平面PAB所成锐二面角的余弦值.
【答案】
(1)证明:∵PB=PC=AB=2,AC=4,BC=2 ![]() ,PA=
,PA= ![]() ,
,
∴AB2+BC2=AC2;
∴BC⊥AB;
D,E分别是BC,AC中点;
∴DE∥AB;
∴BC⊥DE;
又PB=PC,D是BC中点;
∴BC⊥PD,DE∩PD=D;
∴BC⊥平面PED
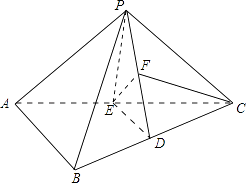
(2)证明:解: PA= ![]() ,PC=2,AC=4,
,PC=2,AC=4,
∴由余弦定理cos∠PCA= ![]() ,
,
在△PCE中,PC=2,CE=2,
∴由余弦定理得PE=1,DE=1,∴PD=1;
∴△PDE为等边三角形;
∴如图,取PD中点F,连接EF,CF,则:EF⊥PD;
又BC⊥平面PED,EF平面PED;
∴BC⊥EF,即EF⊥BC,PD∩BC=D;
∴EF⊥平面PBC;
∴∠ECF是直线AC和平面PBC所成角;
EF= ![]() ,CE=2;
,CE=2;
∴sin∠ECF= ![]() =
= ![]() =
= ![]() ,
,
∴直线AC与平面PBC所成角为arcsin ![]()
(3)证明:以D为原点,分别以DC,DE为x,y轴,建立如图所示的空间直角坐标系,
B(﹣ ![]() ,0,0),C(
,0,0),C( ![]() ,0,0),E(0,1,0),A(﹣
,0,0),E(0,1,0),A(﹣ ![]() ,2,0),
,2,0),
设P(0,y,z),则由PC=2,PA= ![]() ,
,
得 ![]() ,解得y=
,解得y= ![]() ,z=
,z= ![]() ,∴P(0,
,∴P(0, ![]() ),
),
设平面PAB的法向量 ![]() =(x1,y1,z1),
=(x1,y1,z1),
∵ ![]() =(0,2,0),
=(0,2,0), ![]() =(
=( ![]() ),
),
∴  ,取x11,得
,取x11,得 ![]() =(1,0,﹣2),
=(1,0,﹣2),
平面PED的法向量为 ![]() =(1,0,0),
=(1,0,0),
∴cos< ![]() >
>
= ![]() ,
,
∴平面PED与平面PAB所成锐二面角的余弦值为 ![]()
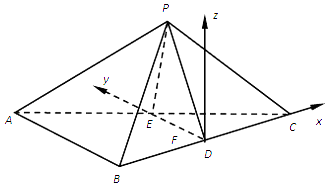
【解析】(1)根据AB,BC,AC边的长度容易得到BC⊥AB,E,D都是中点,从而DE∥AB,这便得到BC⊥DE,而由PB=PC,D为BC边中点,从而便得到BC⊥PD,从而由线面垂直的判定定理即得BC⊥平面PED;(2)取PD中点F,连接EF,CF,则∠ECF是直线AC和平面PBC所成角,由此能求出直线AC与平面PBC所成角.(3)以D为原点,分别以DC,DE为x,y轴,建立空间直角坐标系,利用向量法能求出平面PED与平面PAB所成锐二面角的余弦值.
【考点精析】利用平面与平面垂直的判定和空间角的异面直线所成的角对题目进行判断即可得到答案,需要熟知一个平面过另一个平面的垂线,则这两个平面垂直;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则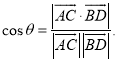 .
.

 阅读快车系列答案
阅读快车系列答案