题目内容
【题目】已知![]() .
.
(1)当![]() 时,若函数
时,若函数![]() 在
在![]() 处的切线与函数
处的切线与函数![]() 相切,求实数
相切,求实数![]() 的值;
的值;
(2)当![]() 时,记
时,记![]() .证明:当
.证明:当![]() 时,存在
时,存在![]() ,使得
,使得![]() .
.
【答案】(1) ![]() .
.
(2)见解析.
【解析】分析:第一问将![]() 代入解析式,之后对函数求导,从而可以求得
代入解析式,之后对函数求导,从而可以求得![]() ,结合
,结合![]() ,利用点斜式写出切线的方程,之后再结合直线与抛物线相切的有关特征求得参数b的值;第二问结合题中的条件,转化函数解析式,利用导数研究函数的性质,向最值靠拢即可证得结果.
,利用点斜式写出切线的方程,之后再结合直线与抛物线相切的有关特征求得参数b的值;第二问结合题中的条件,转化函数解析式,利用导数研究函数的性质,向最值靠拢即可证得结果.
详解:(Ⅰ)解:当![]() 时,
时,![]() ,
,![]()
![]()
![]() ,故切线方程为
,故切线方程为![]() .
.
设切线与![]() 相切的切点为
相切的切点为![]() ,
,
故满足方程组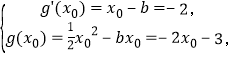
解得![]() ,故
,故![]() .
.
(Ⅱ)证明:![]() ,
,![]()
![]()
![]()
![]()
令![]() ,则
,则![]()
![]()
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
![]()
![]()
![]()
![]() 即
即![]() 恒成立,
恒成立,
![]()
![]() 或
或![]() ,
,
![]()
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]()
![]() .
.
只需证![]() 时,
时,![]() 即可,
即可,
令![]()
则![]() ,
,![]() 恒成立,
恒成立,
![]()
![]() 在
在![]() 上单调递减.
上单调递减.
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() 在
在![]() 上单调递增,
上单调递增,![]() 上单调递减,
上单调递减,
![]()
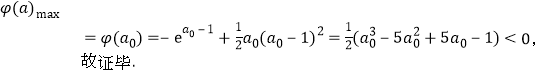

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目