某几何体的正视图与俯视图都是边长为1的正方形.且体积为$\frac{1}{2}$.则该几何体的侧视图可以是( )A．B．C．D．题目和参考答案——青夏教育精英家教网—

题目内容

20．某几何体的正视图与俯视图都是边长为1的正方形，且体积为$\frac{1}{2}$，则该几何体的侧视图可以是（　　）

A．

B．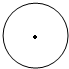

C．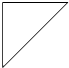

D．

分析不妨令该几何体是一个柱体，由主视图与左视图都是边长为1的正方形，可得底面积为$\frac{1}{2}$，进而得到答案．

解答解：∵某几何体的主视图与左视图都是边长为1的正方形，
故几何体的高为1，
若该几何为柱体，由体积为$\frac{1}{2}$，可得底面积为$\frac{1}{2}$，
此时该几何体的侧视图可以是腰为1的等腰直角三角形，
故选：C．

点评本题考查的知识点是简单空间图形的三视图，考查空间想象能力，难度不大，属于基础题．

练习册系列答案

11．对?x∈（0，$\frac{π}{2}$），下列四个命题：①sinx+tanx＞2x；②sinx•tanx＞x²；③sinx+tanx＞$\frac{8}{3}$x；④sinx•tanx＞2x²，则正确命题的序号是（　　）

8．已知正数a，b满足a+3b=5ab，实数x，y满足$\left\{\begin{array}{l}{x-y≤2}\\{x+2y≥5}\\{y-2≤0}\end{array}\right.$，若z=ax+by，求当3a+4b取最小值时z的最大值．

15．已知z为复数，（1-i）²z=（1+i）³（i为虚数单位），则$\overline z$=（　　）

5．已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点为F，A为短轴的一个端点，且|OA|=|OF|=$\sqrt{2}$（其中O为坐标原点）．
（Ⅰ）求椭圆的方程；
（Ⅱ）若C、D分别是椭圆长轴的左、右端点，动点M满足MD⊥CD，连结CM交椭圆于点P，试问：x轴上是否存在异于点C的定点Q，使得以MP为直径的圆经过直线OP、MQ的交点；若存在，求出点Q的坐标，若不存在，说明理由．

12．将函数f（x）=3sin（2x+θ）（-$\frac{π}{2}$＜θ＜$\frac{π}{2}$）的图象向右平移φ（φ＞0）个单位长度后得到函数g（x）的图象，若f（x），g（x）的图象都经过点P（0，$\frac{3\sqrt{2}}{2}$），则φ的值不可能是（　　）

9．已知圆的方程为（x-1）²+（y+1）²=4，求过圆外一点P（3，2）的切线方程．

10．已知全集U=R，集合A={x∈R|-2≤2x≤1}，集合B={x∈R||x|＜1}，则C_U（A∩B）=（　　）

A．

（-∞，-1]∪（$\frac{1}{2}$，+∞）

B．

（-1，$\frac{1}{2}$]

C．

（-∞，-1）∪[-$\frac{1}{2}$，+∞）

D．

（-1，-$\frac{1}{2}$）

试题分类