题目内容
【题目】定义在D上的函数![]() ,若满足:
,若满足: ![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是D上的有界函数,其中M称为函数
是D上的有界函数,其中M称为函数![]() 的上界.
的上界.
(I)设![]() ,证明:
,证明: ![]() 在
在![]() 上是有界函数,并写出
上是有界函数,并写出![]() 所有上界的值的集合;
所有上界的值的集合;
(II)若函数![]() 在
在![]() 上是以3为上界的有界函数,求实数a的取值范围.
上是以3为上界的有界函数,求实数a的取值范围.
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】试题分析:
(1)由题意结合函数的单调性即可证得结论,且![]() 所有上界的值的集合是
所有上界的值的集合是![]() ;
;
(2)利用题意得到关于实数a的不等式,求解不等式可得实数a的取值范围是![]() .
.
试题解析:
(I)证明:因为![]() ,
,
所以![]() 在
在![]() 上是增函数. 所以
上是增函数. 所以![]() . 即
. 即![]() ,
,
所以![]() ,所以
,所以![]() 是有界函数.
是有界函数.
所以,上界M满足M≥1,所有上界M的集合为![]() ..
..
(II)解:因为函数![]() 在
在![]() 上是以3为上界的有界函数,
上是以3为上界的有界函数,
所以![]() 在
在![]() 上恒成立.
上恒成立.
所以![]() ,
, ![]() ,
,
令![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上恒成立,
上恒成立,
所以, ![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,则
,则![]() 在
在![]() 上是减函数,
上是减函数,
所以![]() ;
;
令![]() ,则
,则![]() 在
在![]() 上是增函数,
上是增函数,
所以![]() ,.
,.
所以,实数a的取值范围![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】为了对2016年某校中考成绩进行分析,在60分以上的全体同学中随机抽出8位,他们的数学分数(已折算为百分制)从小到大排是60、65、70、75、80、85、90、95,物理分数从小到大排是72、77、80、84、88、90、93、95.
(1)若规定85分(包括85分)以上为优秀,求这8位同学中恰有3位同学的数学和物理分数均为优秀的概率;
(2)若这8位同学的数学、物理、化学分数事实上对应如下表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学分数 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
物理分数 | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
化学分数 | 67 | 72 | 76 | 80 | 84 | 87 | 90 | 92 |
①用变量![]() 与
与![]() 与
与![]() 的相关系数说明物理与数学、化学与数学的相关程度;
的相关系数说明物理与数学、化学与数学的相关程度;
②求![]() 与
与![]() 与
与![]() 的线性回归方程(系数精确到0.01),当某同学的数学成绩为50分时,估计其物理、化学两科的得分.
的线性回归方程(系数精确到0.01),当某同学的数学成绩为50分时,估计其物理、化学两科的得分.
参考公式:相关系数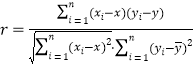 ,
,
回归直线方程是:![]() ,其中
,其中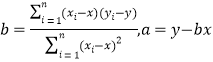 ,
,
参考数据: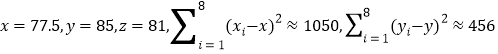 ,
,![]() ,
,![]() ,
,
![]() .
.
【题目】(本小题满分10分,第(1)问 5分,第(2)问 5 分)
近年来,微信越来越受欢迎,许多人通过微信表达自己、交流思想和传递信息,微信是现代生活中进行信息交流的重要工具.而微信支付为用户带来了全新的支付体验,支付环节由此变得简便而快捷.某商场随机对商场购物的![]() 名顾客进行统计,其中
名顾客进行统计,其中![]() 岁以下占
岁以下占![]() ,采用微信支付的占
,采用微信支付的占![]() ,
, ![]() 岁以上采用微信支付的占
岁以上采用微信支付的占![]() 。
。
(1)请完成下面![]() 列联表:
列联表:
|
| 合计 | |
使用微信支付 | |||
未使用微信支付 | |||
合计 |
(2)并由列联表中所得数据判断有多大的把握认为“使用微信支付与年龄有关”?
参考公式:  ,
, ![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|