题目内容
(本大题满分13分)如图,现有一块半径为2m,圆心角为 的扇形铁皮
的扇形铁皮 ,欲从其中裁剪出一块内接五边形
,欲从其中裁剪出一块内接五边形 ,使点
,使点 在
在 弧上,点
弧上,点 分别在半径
分别在半径 和
和 上,四边形
上,四边形 是矩形,点
是矩形,点 在弧
在弧 上,
上, 点在线段
点在线段 上,四边形
上,四边形 是直角梯形.现有如下裁剪方案:先使矩形
是直角梯形.现有如下裁剪方案:先使矩形 的面积达到最大,在此前提下,再使直角梯形
的面积达到最大,在此前提下,再使直角梯形 的面积也达到最大.
的面积也达到最大.
(Ⅰ)设 ,当矩形
,当矩形 的面积最大时,求
的面积最大时,求 的值;
的值;
(Ⅱ)求按这种裁剪方法的原材料利用率.

 的扇形铁皮
的扇形铁皮 ,欲从其中裁剪出一块内接五边形
,欲从其中裁剪出一块内接五边形 ,使点
,使点 在
在 弧上,点
弧上,点 分别在半径
分别在半径 和
和 上,四边形
上,四边形 是矩形,点
是矩形,点 在弧
在弧 上,
上, 点在线段
点在线段 上,四边形
上,四边形 是直角梯形.现有如下裁剪方案:先使矩形
是直角梯形.现有如下裁剪方案:先使矩形 的面积达到最大,在此前提下,再使直角梯形
的面积达到最大,在此前提下,再使直角梯形 的面积也达到最大.
的面积也达到最大.(Ⅰ)设
 ,当矩形
,当矩形 的面积最大时,求
的面积最大时,求 的值;
的值;(Ⅱ)求按这种裁剪方法的原材料利用率.

解:(Ⅰ)先求矩形 面积的最大值:
面积的最大值:
设
 ,
, ,则
,则 ,
,
 ,∴当
,∴当 ,即
,即 时,
时,
此时, ,
, ……………………6分
……………………6分
(Ⅱ)过Q点作 垂足为S,设
垂足为S,设
在 中,有
中,有 ,
,
则 ,
,
∴
 ……… 8分
……… 8分
令 ,∵
,∵ ,∴
,∴ ,
,
此时 ,则
,则 ,
,
当 时,
时, 的最大值为
的最大值为 ………………………… 10分
………………………… 10分
∴方案裁剪出内接五边形 面积最大值为
面积最大值为
 ,即利用率=
,即利用率= ……12分
……12分
 面积的最大值:
面积的最大值:设

 ,
, ,则
,则 ,
, ,∴当
,∴当 ,即
,即 时,
时,
此时,
 ,
, ……………………6分
……………………6分(Ⅱ)过Q点作
 垂足为S,设
垂足为S,设
在
 中,有
中,有 ,
,则
 ,
,∴

 ……… 8分
……… 8分令
 ,∵
,∵ ,∴
,∴ ,
,此时
 ,则
,则 ,
,当
 时,
时, 的最大值为
的最大值为 ………………………… 10分
………………………… 10分∴方案裁剪出内接五边形
 面积最大值为
面积最大值为
 ,即利用率=
,即利用率= ……12分
……12分略

练习册系列答案
相关题目
 ,
, ).
). |=|
|=| |,求角α的值;
|,求角α的值; 的值.
的值. 成立;
成立; -2x)是偶函数;
-2x)是偶函数;  是函数y=sin(2x+
是函数y=sin(2x+ )的图象的一条对称轴的方程.
)的图象的一条对称轴的方程. 的部分图象如图所示,则
的部分图象如图所示,则 的图象可由函数
的图象可由函数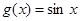 的图象(纵坐标不变)变换如下
的图象(纵坐标不变)变换如下
 倍,再向右平移
倍,再向右平移 个单位
个单位 个单位
个单位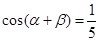 ,
, ,则
,则
 =____
=____  ,若函数
,若函数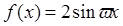 在
在 上单调递增,则
上单调递增,则 的取值范围是___
的取值范围是___ 且
且 ,,则
,,则 的值是( )
的值是( )



 ,且
,且 ,则
,则 ;
; 的单调递减区间是___________▲_____________.
的单调递减区间是___________▲_____________.