题目内容
11.设F为抛物线C:y2=2px的焦点,过F且倾斜角为60°的直线交曲线C于A,B两点(B点在第一象限,A点在第四象限),O为坐标原点,过A作C的准线的垂线,垂足为M,则|OB|与|OM|的比为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 3 | D. | 4 |
分析 求得抛物线的焦点和准线方程,设出直线AB的方程,代入抛物线方程,消去x,求得y1=-$\frac{\sqrt{3}}{3}$p,y2=$\sqrt{3}$p,运用两点的距离公式,计算即可得到结论.
解答 解:抛物线C:y2=2px的焦点F($\frac{p}{2}$,0),
准线为x=-$\frac{p}{2}$,
设直线AB:y=$\sqrt{3}$(x-$\frac{p}{2}$),
联立抛物线方程,消去x,可得
$\sqrt{3}$y2-2py-$\sqrt{3}$p2=0,
设A(x1,y1),B(x2,y2),
则y1=-$\frac{\sqrt{3}}{3}$p,y2=$\sqrt{3}$p,
由M(-$\frac{p}{2}$,y1),
则|OM|=$\sqrt{\frac{{p}^{2}}{4}+{{y}_{1}}^{2}}$=$\sqrt{\frac{{p}^{2}}{4}+\frac{{p}^{2}}{3}}$=$\frac{\sqrt{21}}{6}$p,
|OB|=$\sqrt{{{x}_{2}}^{2}+{{y}_{2}}^{2}}$=$\sqrt{\frac{{{y}_{2}}^{4}}{4{p}^{2}}+{{y}_{2}}^{2}}$=$\sqrt{\frac{9{p}^{4}}{4{p}^{2}}+3{p}^{2}}$=$\frac{\sqrt{21}}{2}$p,
即有|OB|=3|OM|.
故选C.
点评 本题考查抛物线的方程和性质,主要考查抛物线的焦点和准线方程的运用,同时考查直线和抛物线联立,求得交点,考查运算能力,属于中档题.

练习册系列答案
相关题目
2.已知S=$\frac{π}{200000}$(sin$\frac{π}{200000}$+sin$\frac{2π}{200000}$+sin$\frac{3π}{200000}$+…+sin$\frac{100000π}{200000}$),推测下列各值中与S最接近的是( )
| A. | 0.9988 | B. | 0.9999 | C. | 1.0001 | D. | 2.0002 |
19.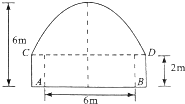 要设计一个隧道,在隧道内设双行线公路,其截面由一个长方形和抛物线构成(如图所示),若车道总宽度AB为6m,通过车辆(设为平顶)限高3.5米,且车辆顶部与隧道顶部在竖直方向上的高度只差至少为0.5m,则隧道的拱宽CD至少应设计为(精确到0.1m.)( )参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732.
要设计一个隧道,在隧道内设双行线公路,其截面由一个长方形和抛物线构成(如图所示),若车道总宽度AB为6m,通过车辆(设为平顶)限高3.5米,且车辆顶部与隧道顶部在竖直方向上的高度只差至少为0.5m,则隧道的拱宽CD至少应设计为(精确到0.1m.)( )参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732.
 要设计一个隧道,在隧道内设双行线公路,其截面由一个长方形和抛物线构成(如图所示),若车道总宽度AB为6m,通过车辆(设为平顶)限高3.5米,且车辆顶部与隧道顶部在竖直方向上的高度只差至少为0.5m,则隧道的拱宽CD至少应设计为(精确到0.1m.)( )参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732.
要设计一个隧道,在隧道内设双行线公路,其截面由一个长方形和抛物线构成(如图所示),若车道总宽度AB为6m,通过车辆(设为平顶)限高3.5米,且车辆顶部与隧道顶部在竖直方向上的高度只差至少为0.5m,则隧道的拱宽CD至少应设计为(精确到0.1m.)( )参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732.| A. | 8.9m | B. | 8.5m | C. | 8.2m | D. | 7.9m |
6.在极坐标系中,与曲线ρ=cosθ+1关于直线θ=$\frac{π}{6}$(ρ∈R)对称的曲线的极坐标方程是( )
| A. | ρ=sin($\frac{π}{3}$+θ)+1 | B. | ρ=sin($\frac{π}{3}$-θ)+1 | C. | ρ=sin($\frac{π}{6}$+θ)+1 | D. | ρ=sin($\frac{π}{6}$-θ)+1 |
16.已知i是虚数单位,若复数z满足z=$\frac{25}{3-4i}$,则z的共轭复数$\overline{z}$为( )
| A. | -3+4i | B. | -3-4i | C. | 3+4i | D. | 3-4i |
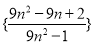 .
.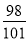 是不是该数列中的项,为什么?
是不是该数列中的项,为什么?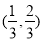 内有、无数列中的项?若有,有几项?若没有,说明理由.
内有、无数列中的项?若有,有几项?若没有,说明理由.