题目内容
已知函数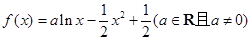 .
.
(Ⅰ)求 的单调区间;
的单调区间;
(Ⅱ)是否存在实数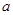 ,使得对任意的
,使得对任意的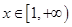 ,都有
,都有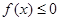 ?若存在,求
?若存在,求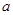 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
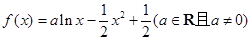 .
.(Ⅰ)求
 的单调区间;
的单调区间;(Ⅱ)是否存在实数
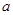 ,使得对任意的
,使得对任意的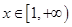 ,都有
,都有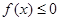 ?若存在,求
?若存在,求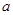 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.Ⅰ) 的定义域为
的定义域为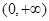 .
. 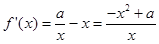 . ………2分
. ………2分
当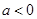 时,在区间
时,在区间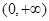 上,
上,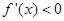 .
.
所以 的单调递减区间是
的单调递减区间是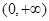 . ……………………………3分
. ……………………………3分
当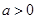 时,令
时,令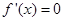 得
得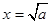 或
或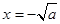 (舍).
(舍).
函数 ,
,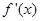 随
随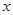 的变化如下:
的变化如下:
所以  的单调递增区间是
的单调递增区间是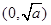 ,单调递减区间是
,单调递减区间是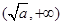 . ……6分
. ……6分
综上所述,当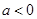 时,
时,  的单调递减区间是
的单调递减区间是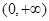 ;
;
当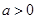 时,
时, 的单调递增区间是
的单调递增区间是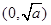 ,单调递减区间是
,单调递减区间是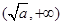 .
.
(Ⅱ)由(Ⅰ)可知:当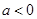 时,
时,  在
在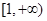 上单调递减.
上单调递减.
所以 在
在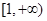 上的最大值为
上的最大值为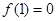 ,即对任意的
,即对任意的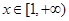 ,都有
,都有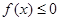 . ……………7分 当
. ……………7分 当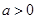 时,
时,
① 当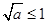 ,即
,即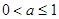 时,
时, 在
在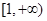 上单调递减.
上单调递减.
所以 在
在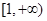 上的最大值为
上的最大值为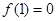 ,即对任意的
,即对任意的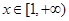 ,都有
,都有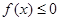 .
.
当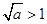 ,即
,即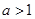 时,
时, 在
在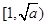 上单调递增,所以
上单调递增,所以 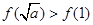 .又
.又 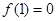 ,所以
,所以 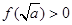 ,与对于任意的
,与对于任意的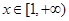 ,都有
,都有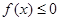 矛盾. ……12分
矛盾. ……12分
综上所述,存在实数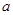 满足题意,此时
满足题意,此时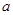 的取值范围是
的取值范围是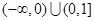 .
.
 的定义域为
的定义域为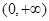 .
. 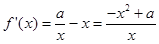 . ………2分
. ………2分当
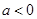 时,在区间
时,在区间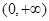 上,
上,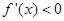 .
. 所以
 的单调递减区间是
的单调递减区间是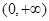 . ……………………………3分
. ……………………………3分当
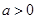 时,令
时,令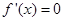 得
得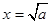 或
或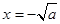 (舍).
(舍).函数
 ,
,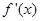 随
随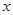 的变化如下:
的变化如下: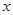 | 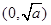 | 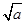 | 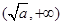 |
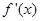 | + | 0 | 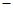 |
 | ↗ | 极大值 | ↘ |
 的单调递增区间是
的单调递增区间是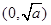 ,单调递减区间是
,单调递减区间是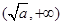 . ……6分
. ……6分综上所述,当
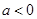 时,
时,  的单调递减区间是
的单调递减区间是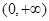 ;
;当
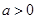 时,
时, 的单调递增区间是
的单调递增区间是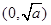 ,单调递减区间是
,单调递减区间是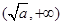 .
.(Ⅱ)由(Ⅰ)可知:当
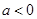 时,
时,  在
在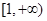 上单调递减.
上单调递减.所以
 在
在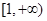 上的最大值为
上的最大值为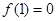 ,即对任意的
,即对任意的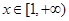 ,都有
,都有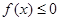 . ……………7分 当
. ……………7分 当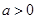 时,
时,① 当
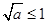 ,即
,即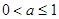 时,
时, 在
在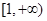 上单调递减.
上单调递减. 所以
 在
在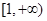 上的最大值为
上的最大值为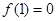 ,即对任意的
,即对任意的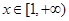 ,都有
,都有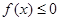 .
. 当
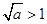 ,即
,即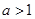 时,
时, 在
在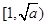 上单调递增,所以
上单调递增,所以 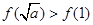 .又
.又 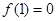 ,所以
,所以 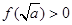 ,与对于任意的
,与对于任意的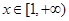 ,都有
,都有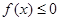 矛盾. ……12分
矛盾. ……12分综上所述,存在实数
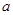 满足题意,此时
满足题意,此时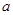 的取值范围是
的取值范围是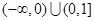 .
.略

练习册系列答案
相关题目

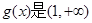 上的增函数,求k的取值范围;
上的增函数,求k的取值范围; 求满足条件的最大整数k的值。
求满足条件的最大整数k的值。 。
。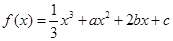 有两个极值点
有两个极值点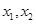 且
且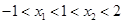 ,则直线
,则直线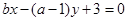 的斜率的取值范围是( )
的斜率的取值范围是( ) 



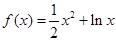 .
.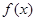 在区间
在区间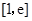 上的最大、最小值;
上的最大、最小值;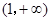 上,函数
上,函数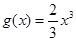 的图象的下方
的图象的下方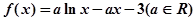 .
.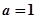 时,求函数
时,求函数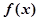 的单调区间;
的单调区间;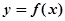 的图像在点
的图像在点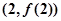 处的切线的倾斜角为
处的切线的倾斜角为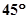 ,问:m在什么范围取值时,对于任意的
,问:m在什么范围取值时,对于任意的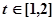 ,函数
,函数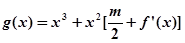 在区间
在区间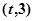 上总存在极值?
上总存在极值?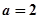 时,设函数
时,设函数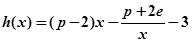 ,若在区间
,若在区间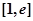 上至少存在一个
上至少存在一个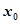 ,使得
,使得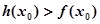 成立,试求实数p的取值范围.
成立,试求实数p的取值范围.
 的图象在点
的图象在点 处的切线方程为
处的切线方程为 ,求
,求 在区间
在区间 上的最大值;
上的最大值; 时,若
时,若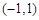 上不单调,求
上不单调,求 的取值范围.
的取值范围.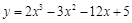 在[0,3]上的最大值和最小值分别是
在[0,3]上的最大值和最小值分别是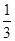 x3+81x-234,则使该生产厂家获取最大年利润的年产量为( )
x3+81x-234,则使该生产厂家获取最大年利润的年产量为( )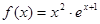 ,
,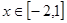 的最大值为
的最大值为