题目内容
已知函数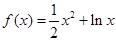 .
.
(1)求函数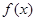 在区间
在区间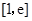 上的最大、最小值;
上的最大、最小值;
(2)求证:在区间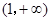 上,函数
上,函数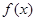 的图象在函数
的图象在函数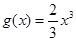 的图象的下方
的图象的下方
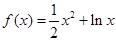 .
.(1)求函数
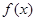 在区间
在区间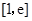 上的最大、最小值;
上的最大、最小值;(2)求证:在区间
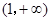 上,函数
上,函数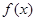 的图象在函数
的图象在函数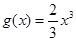 的图象的下方
的图象的下方(1)由已知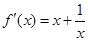 ,
,
当 时,
时,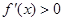 ,
,
所以函数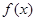 在区间
在区间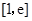 上单调递增,
上单调递增,
所以函数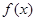 在区间
在区间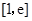 上的最大、最小值分别为
上的最大、最小值分别为 ,
, ,
,
所以函数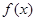 在区间
在区间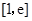 上的最大值为
上的最大值为 ,最小值为
,最小值为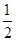 ;
;
(2)证明:设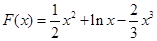 ,则
,则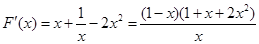 .
.
因为 ,所以
,所以 ,
,
所以函数 在区间
在区间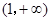 上单调递减,
上单调递减,
又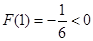 ,所以在区间
,所以在区间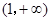 上,
上,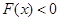 ,即
,即 ,
,
所以在区间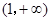 上函数
上函数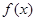 的图象在函数
的图象在函数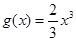 图象的下方.
图象的下方.
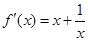 ,
,当
 时,
时,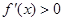 ,
,所以函数
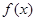 在区间
在区间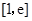 上单调递增,
上单调递增,所以函数
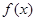 在区间
在区间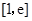 上的最大、最小值分别为
上的最大、最小值分别为 ,
, ,
,所以函数
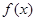 在区间
在区间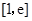 上的最大值为
上的最大值为 ,最小值为
,最小值为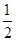 ;
;(2)证明:设
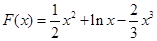 ,则
,则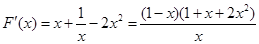 .
.因为
 ,所以
,所以 ,
,所以函数
 在区间
在区间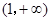 上单调递减,
上单调递减,又
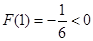 ,所以在区间
,所以在区间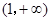 上,
上,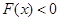 ,即
,即 ,
,所以在区间
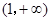 上函数
上函数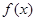 的图象在函数
的图象在函数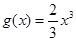 图象的下方.
图象的下方.(1)求闭区间上函数的最值,只需要利用导数求出极值,然后与区间的端点值进行比较从而可确定其最大值和最小值.
(2)本小题可构造函数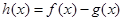 ,然后证明h(x)在
,然后证明h(x)在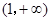 上恒小于零即可,进而利用导数研究h(x)的最小值问题得解.
上恒小于零即可,进而利用导数研究h(x)的最小值问题得解.
(2)本小题可构造函数
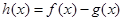 ,然后证明h(x)在
,然后证明h(x)在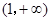 上恒小于零即可,进而利用导数研究h(x)的最小值问题得解.
上恒小于零即可,进而利用导数研究h(x)的最小值问题得解.
练习册系列答案
相关题目
 (
(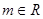 ),
),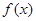 的导数为
的导数为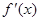 ,且
,且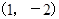
 ,若
,若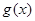 在
在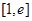 的最小值是2,求实数
的最小值是2,求实数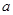 的值.
的值.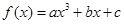 在
在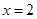 处取得极值为
处取得极值为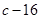
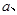
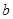 的值;(2)若
的值;(2)若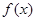 有极大值28,求
有极大值28,求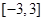 上的最小值.
上的最小值.
 时,求曲线
时,求曲线 处的切线方程;
处的切线方程; 时,求
时,求 的极大值和极小值;
的极大值和极小值; 上是增函数,求实数
上是增函数,求实数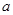 的取值范围.
的取值范围.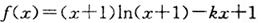 ,,k为常数,e是自然对数的底数).
,,k为常数,e是自然对数的底数).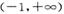 上的图象均在第一、二象限?若存在,求出k的最大值;若不存在,请说明理由;
上的图象均在第一、二象限?若存在,求出k的最大值;若不存在,请说明理由;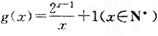 ,记
,记 ,求证:
,求证: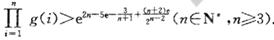
 )内是增函数,则实数a的取值范围是( )
)内是增函数,则实数a的取值范围是( ) 3;
3; 3
3
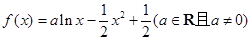 .
. 的单调区间;
的单调区间;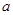 ,使得对任意的
,使得对任意的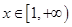 ,都有
,都有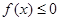 ?若存在,求
?若存在,求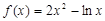 的单调递增区间是 。
的单调递增区间是 。