题目内容
11.已知二次函数f(x)满足f(x+1)-f(x)=4x,且f(0)=1.(1)求二次函数f(x)的解析式.
(2)求函数g(x)=($\frac{1}{2}$)f(x)的单调增区间和值域.
分析 (1)利用待定系数法即可求二次函数f(x)的解析式.
(2)利用换元法结合复合函数单调性的关系结合一元二次函数和指数函数的性质进行求解即可.
解答 解:(1)设二次函数f(x)=ax2+bx+c(a≠0).…(1分)
∵f(0)=1,∴c=1.把f(x)的表达式代入f(x+1)-f(x)=4x,有
a(x+1)2+b(x+1)+1-(ax2+bx+1)=4x.…(3分)
∴2ax+a+b=4x.∴a=2,b=-2.…(5分)
∴f(x)=2x2-2x+1.…(6分)
(2)g(x)=($\frac{1}{2}$)f(x)=$(\frac{1}{2})^{2{x}^{2}-2x+1}$,
令t=2x2-2x+1,则t=2x2-2x+1=2(x-$\frac{1}{2}$)2+$\frac{1}{2}$…(8分)
此时y=($\frac{1}{2}$)t为减函数,
当x≥$\frac{1}{2}$时,函数t=2x2-2x+1为增函数,此时g(x)为减函数,即函数单调递减区间为(-∞,$\frac{1}{2}$],
当x≤$\frac{1}{2}$时,函数t=2x2-2x+1为减函数,此时g(x)为增函数,即函数单调递增区间为[$\frac{1}{2}$,+∞),
∵t=2x2-2x+1=2(x-$\frac{1}{2}$)2+$\frac{1}{2}$≥$\frac{1}{2}$,
∴0<($\frac{1}{2}$)t≤=($\frac{1}{2}$)${\;}^{\frac{1}{2}}$=$\frac{\sqrt{2}}{2}$,
即函数的值域为(0,$\frac{\sqrt{2}}{2}$].…(12分)
点评 本题主要考查一元二次函数解析式的求解,以及复合函数单调性和单调区间的求解和判断,利用换元法结合指数函数和一元二次函数的性质是解决本题的关键.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案| A. | (-∞,-e+$\frac{3}{2}$] | B. | [-e+$\frac{3}{2}$,e] | C. | [-e,e] | D. | [e,+∞) |
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
| A. | $\frac{3\sqrt{17}}{2}$ | B. | $\frac{6}{7}$$\sqrt{17}$ | C. | 3$\sqrt{17}$ | D. | $\frac{9}{14}$$\sqrt{17}$ |
| A. | R | B. | (0,+∞) | C. | (-∞,0) | D. | {x|x≠0} |
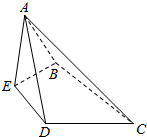 等边△ABC中,D,E分别是AC,AB的中点,沿DE将△ADE折起,使平面ADE⊥平面BCDE(如图所示).
等边△ABC中,D,E分别是AC,AB的中点,沿DE将△ADE折起,使平面ADE⊥平面BCDE(如图所示).