题目内容
20.直线l:4x-y-4=0与l1:x-2y-2=0及l2:4x+3y-12=0所得两交点的距离为( )| A. | $\frac{3\sqrt{17}}{2}$ | B. | $\frac{6}{7}$$\sqrt{17}$ | C. | 3$\sqrt{17}$ | D. | $\frac{9}{14}$$\sqrt{17}$ |
分析 求出两条直线的交点坐标,利用两点间的距离公式进行求解即可.
解答 解:由$\left\{\begin{array}{l}{4x-y-4=0}\\{x-2y-2=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{6}{7}}\\{y=-\frac{4}{7}}\end{array}\right.$,即A($\frac{6}{7}$,$-\frac{4}{7}$ )
由$\left\{\begin{array}{l}{4x-y-4=0}\\{4x+3y-12=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=2}\end{array}\right.$,即B($\frac{3}{2}$,2),
则|AB|=$\sqrt{(\frac{6}{7}-\frac{3}{2})^{2}+(-\frac{4}{7}-2)^{2}}$=$\sqrt{(\frac{9}{14})^{2}+(\frac{36}{14})^{2}}$=$\frac{9}{14}$$\sqrt{17}$,
故选:D.
点评 本题主要考查直线的交点坐标的计算,以及两点间距离公式的应用,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.下面几种推理过程是演绎推理的是( )
| A. | 两条直线平行,同旁内角互补,如果∠A和∠B是两条平行直线的同旁内角,则∠A+∠B=180° | |
| B. | 由平面三角形的性质,推测空间四面体的性质 | |
| C. | 某校高三共有10个班,1班有51人,2班有53人,三班有52人,由此推测各班都超过50人 | |
| D. | 在数列{an}中,a1=1,an=$\frac{1}{2}$(an-1+$\frac{1}{{a}_{n-1}}$)(n≥2),计算a2、a3,a4,由此猜测通项an |
15.设f:A→B是从集合A到集合B的映射,则下列说法正确的是( )
| A. | A中不同元素的像必不同 | |
| B. | A中每一个元素在B中必有像 | |
| C. | B中每一个元素在A中必有原像 | |
| D. | B中每一个元素在A中必有唯一的原像 |
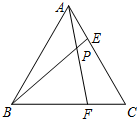 等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连结AF,BE相交于点P.
等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连结AF,BE相交于点P.