Question

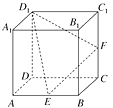
【题目】已知三棱柱ABC-A′B′C′，底面是边长为1的正三角形，侧面为全等的矩形且高为8，求一点自A点出发沿着三棱柱的侧面绕行一周后到达A′点的最短路线长.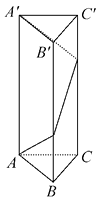

本题条件不变，求一点自A点出发沿着三棱柱的侧面绕行两周后到达A′点的最短路线长.

Answer 1

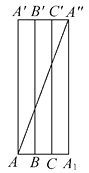
【答案】解：将三棱柱侧面沿侧棱AA′剪开，展成平面图形如图，则AA″即为所求的最短路线.

在Rt△AA1A″中，AA1=3，A1A″=8，所以AA″= = .

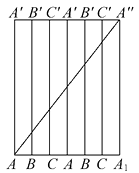
将两个相同的题目中的三棱柱的侧面都沿AA′剪开，然后展开并拼接成如图所示，则AA″即为所求的最短路线.在Rt△AA1A″中，AA1=6，A1A″=8，

所以AA″= = =10.

【解析】考察“最短路线长”一般是求几何体侧面展开图像的对角线的距离。根据已知条件结合勾股定理即可得出。
【考点精析】解答此题的关键在于理解棱柱的结构特征的相关知识，掌握两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形．