题目内容
函数f(x)=
(1)求f(-3);f[f(-5)];
(2)画出函数f(x)的图象,并求出值域;
(3)若f(a)=
,求a的值.
|
(1)求f(-3);f[f(-5)];
(2)画出函数f(x)的图象,并求出值域;
(3)若f(a)=
| 1 |
| 2 |
考点:函数的图象,函数的值
专题:函数的性质及应用
分析:(1)代入求出函数的值即可,
(2)画出图象,由图象得到值域,
(3)根据条件分别求出a的值
(2)画出图象,由图象得到值域,
(3)根据条件分别求出a的值
解答:
 解:(1)f(-3)=-3+5=2,f(-5)=-5+5=0,f(0)=0,f[f(-5)]=0
解:(1)f(-3)=-3+5=2,f(-5)=-5+5=0,f(0)=0,f[f(-5)]=0
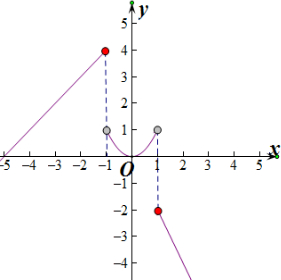
(2)图象如图所示,
由图象可知函数的值域为(-∞,4],
(3)∵f(a)=
,
当x≤-1时,a+5=
,解得a=-
,
当-1<x<1时,a2=
,解得a=±
,
当a≥1时,-2a=
,解得a=-
(舍去)
综上所述a的值为-
,-
,
 解:(1)f(-3)=-3+5=2,f(-5)=-5+5=0,f(0)=0,f[f(-5)]=0
解:(1)f(-3)=-3+5=2,f(-5)=-5+5=0,f(0)=0,f[f(-5)]=0(2)图象如图所示,
由图象可知函数的值域为(-∞,4],
(3)∵f(a)=
| 1 |
| 2 |
当x≤-1时,a+5=
| 1 |
| 2 |
| 9 |
| 2 |
当-1<x<1时,a2=
| 1 |
| 2 |
| ||
| 2 |
当a≥1时,-2a=
| 1 |
| 2 |
| 1 |
| 4 |
综上所述a的值为-
| 9 |
| 2 |
| ||
| 2 |
| ||
| 2 |
点评:本题主要考查了分段函数的问题,以及函数值得求法,以及图象的画法,属于基础题

练习册系列答案
相关题目
如果函数y=f(x)的图象经过点(0,1),那么函数y=f-1(x)+2的反函数的图象过点( )
| A、(3,0) |
| B、(0,3) |
| C、(1,2) |
| D、(2,1) |