题目内容
已知函数f(x)=sinx,g(x)=mx-
(m为实数).
(Ⅰ)求曲线y=f(x)在点P(
,f(
))处的切线方程;
(Ⅱ)求函数g(x)的单调减区间;
(Ⅲ)若m=1,证明:当x>0时,x>f(x)>g(x).
| x3 |
| 6 |
(Ⅰ)求曲线y=f(x)在点P(
| π |
| 4 |
| π |
| 4 |
(Ⅱ)求函数g(x)的单调减区间;
(Ⅲ)若m=1,证明:当x>0时,x>f(x)>g(x).
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)求出函数f(x)的导函数,得到f′(
)的值,求得切点坐标,由直线方程的点斜式得答案;
(Ⅱ)解:求出函数g(x)的导函数g′(x)=m-
x2,然后分m≤0和m>0分析导函数的符号,从而求得g(x)的单调递减区间;
(Ⅲ)分别构造函数h(x)=x-sinx,x∈[0,+∞),t(x)=f(x)-g(x)=sinx-x+
,然后利用其导函数的符号判断所构造函数的单调性,从而证明答案.
| π |
| 4 |
(Ⅱ)解:求出函数g(x)的导函数g′(x)=m-
| 1 |
| 2 |
(Ⅲ)分别构造函数h(x)=x-sinx,x∈[0,+∞),t(x)=f(x)-g(x)=sinx-x+
| x3 |
| 6 |
解答:
(Ⅰ)解:由题意得所求切线的斜率k=f′(
)=cos
=
.
切点P(
,
),则切线方程为y-
=
(x-
),
即x-
y+1-
=0.
(Ⅱ)解:g′(x)=m-
x2.
①当m≤0时,g′(x)≤0,则g(x)的单调递减区间是(-∞,+∞);
②当m>0时,令g′(x)<0,解得x<-
或x>
,
则g(x)的单调递减区间是(-∞,-
),(
,+∞).
(Ⅲ)证明:令h(x)=x-sinx,x∈[0,+∞),h′(x)=1-cosx≥0,
则h(x)是[0,+∞)上的增函数.
故当x>0时,h(x)>h(0)=0,x>sinx,
当m=1时,令t(x)=f(x)-g(x)=sinx-x+
,
则t′(x)=cosx-1+
x2,
而t′′(x)=-sinx+x在x>0时恒大于0,
∴t′(x)为(0,+∞)上的增函数,即t′(x)>t′(0)=0,
即t(x)=f(x)-g(x)在(0,+∞)上为增函数,
∴t(x)=f(x)-g(x)>t(0)=0,
故f(x)>g(x).
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
切点P(
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| π |
| 4 |
即x-
| 2 |
| π |
| 4 |
(Ⅱ)解:g′(x)=m-
| 1 |
| 2 |
①当m≤0时,g′(x)≤0,则g(x)的单调递减区间是(-∞,+∞);
②当m>0时,令g′(x)<0,解得x<-
| 2m |
| 2m |
则g(x)的单调递减区间是(-∞,-
| 2m |
| 2m |
(Ⅲ)证明:令h(x)=x-sinx,x∈[0,+∞),h′(x)=1-cosx≥0,
则h(x)是[0,+∞)上的增函数.
故当x>0时,h(x)>h(0)=0,x>sinx,
当m=1时,令t(x)=f(x)-g(x)=sinx-x+
| x3 |
| 6 |
则t′(x)=cosx-1+
| 1 |
| 2 |
而t′′(x)=-sinx+x在x>0时恒大于0,
∴t′(x)为(0,+∞)上的增函数,即t′(x)>t′(0)=0,
即t(x)=f(x)-g(x)在(0,+∞)上为增函数,
∴t(x)=f(x)-g(x)>t(0)=0,
故f(x)>g(x).
点评:本题考查了利用导数研究过曲线上某点的切线方程,考查了利用导数研究函数的单调性,训练了函数构造法,体现了数学转化思想方法,是压轴题.

练习册系列答案
相关题目
如果函数y=f(x)的图象经过点(0,1),那么函数y=f-1(x)+2的反函数的图象过点( )
| A、(3,0) |
| B、(0,3) |
| C、(1,2) |
| D、(2,1) |
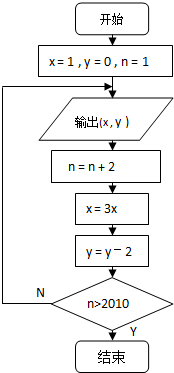 已知某算法的流程图如图所示,若将输出的(x,y 值依次记为(x1,y1),(x2,y2),…(xn,yn),…
已知某算法的流程图如图所示,若将输出的(x,y 值依次记为(x1,y1),(x2,y2),…(xn,yn),…