题目内容
【题目】给出下列四个命题中：
①命题： 
；
②函数f（x）=2x﹣x2有三个零点；
③对（x，y）∈{（x，y）|4x+3y﹣10=0}，则x2+y2≥4．
④已知函数 
，若△ABC中，角C是钝角，那么f（sinA）＞f（cosB）
其中所有真命题的序号是 ．
【答案】①②③④
【解析】解： 
，故①对；
画出函数y=2x ， y=x2的图象如下图，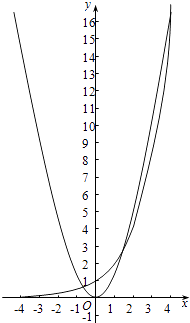
可知②对；
圆x2+y2=4的圆心（0，0）到4x+3y﹣10=0的距离d= 
=2，
故（x，y）∈{（x，y）|4x+3y﹣10=0}，均有x2+y2≥4，
故③正确，
因为 
，
故 
，
所以1＞cosB＞sinA＞0，
又因为f（x）在（0，1）上单调递减．
故f（sinA）＞f（cosB），即④正确；
故真命题的序号有：①②③④，
所以答案是：①②③④．
【考点精析】解答此题的关键在于理解命题的真假判断与应用的相关知识，掌握两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系．
练习册系列答案
相关题目
