题目内容
【题目】团体购买公园门票,票价如下表:
购票人数 | 1~50 | 51~100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
现某单位要组织其市场部和生产部的员工游览该公园,这两个部门人数分别为a和b![]() ,若按部门作为团体,选择两个不同的时间分别购票游览公园,则共需支付门票费为1290元;若两个部门合在一起作为一个团体,同一时间购票游览公园,则需支付门票费为990元,那么这两个部门的人数
,若按部门作为团体,选择两个不同的时间分别购票游览公园,则共需支付门票费为1290元;若两个部门合在一起作为一个团体,同一时间购票游览公园,则需支付门票费为990元,那么这两个部门的人数![]() ____;
____;![]() ____.
____.
【答案】70 40
【解析】
根据990不能被13整除,得两个部门人数之和:a+b≥51,然后结合门票价格和人数之间的关系,建立方程组进行求解即可.
∵990不能被13整除,∴两个部门人数之和:a+b≥51,
(1)若51≤a+b≤100,则11 (a+b)=990得:a+b=90,①
由共需支付门票费为1290元可知,11a+13b=1290 ②
解①②得:b=150,a=﹣60,不符合题意.
(2)若a+b≥100,则9 (a+b)=990,得 a+b=110 ③
由共需支付门票费为1290元可知,1≤a≤50,51≤b≤100,
得11a+13b=1290 ④,
解③④得:a=70人,b=40人,
故答案为:70,40.

【题目】某商场营销人员进行某商品M市场营销调查发现,每回馈消费者一定的点数,该商品每天的销量就会发生一定的变化,经过试点统计得到以如表:
反馈点数t | 1 | 2 | 3 | 4 | 5 |
销量 |
|
| 1 |
|
|
![]() 经分析发现,可用线性回归模型拟合当地该商品销量
经分析发现,可用线性回归模型拟合当地该商品销量![]() 千件
千件![]() 与返还点数t之间的相关关系
与返还点数t之间的相关关系![]() 请用最小二乘法求y关于t的线性回归方程
请用最小二乘法求y关于t的线性回归方程![]() ,并预测若返回6个点时该商品每天销量;
,并预测若返回6个点时该商品每天销量;
![]() 若节日期间营销部对商品进行新一轮调整
若节日期间营销部对商品进行新一轮调整![]() 已知某地拟购买该商品的消费群体十分庞大,经营销调研机构对其中的200名消费者的返点数额的心理预期值进行了一个抽样调查,得到如下一份频数表:
已知某地拟购买该商品的消费群体十分庞大,经营销调研机构对其中的200名消费者的返点数额的心理预期值进行了一个抽样调查,得到如下一份频数表:
返还点数预期值区间
|
|
|
|
|
|
|
频数 | 20 | 60 | 60 | 30 | 20 | 10 |
![]() 求这200位拟购买该商品的消费者对返点点数的心理预期值X的样本平均数及中位数的估计值
求这200位拟购买该商品的消费者对返点点数的心理预期值X的样本平均数及中位数的估计值![]() 同一区间的预期值可用该区间的中点值代替;估计值精确到
同一区间的预期值可用该区间的中点值代替;估计值精确到![]() ;
;
![]() 将对返点点数的心理预期值在
将对返点点数的心理预期值在![]() 和
和![]() 的消费者分别定义为“欲望紧缩型”消费者和“欲望膨胀型”消费者,现采用分层抽样的方法从位于这两个区间的30名消费者中随机抽取6名,再从这6人中随机抽取3名进行跟踪调查,设抽出的3人中“欲望膨胀型”消费者的人数为随机变量X,求X的分布列及数学期望.
的消费者分别定义为“欲望紧缩型”消费者和“欲望膨胀型”消费者,现采用分层抽样的方法从位于这两个区间的30名消费者中随机抽取6名,再从这6人中随机抽取3名进行跟踪调查,设抽出的3人中“欲望膨胀型”消费者的人数为随机变量X,求X的分布列及数学期望.
参考公式及数据: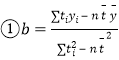 ,
,![]() ;
;![]() .
.