Question

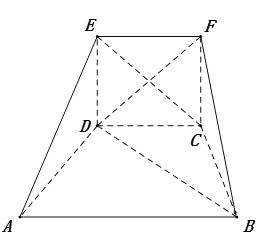
【题目】在如图所示的五面体ABCDEF中，AB∥CD，AB＝2AD＝2，∠ADC＝∠BCD＝120°，四边形EDCF是正方形，二面角E﹣DC﹣A的大小为90°．

（1）求证：直线AD⊥平面BDE

（2）求点D到平面ABE的距离．

Answer 1

【答案】(1)证明见解析 (2)．

【解析】

（1）先证明ED⊥AD，再由余弦定理得BD，根据勾股定理证明AD⊥BD得到证明.

（2）利用等体积法VE﹣ABD＝VD﹣ABE，得到计算得到答案.

（1）证明：因为四边形EDCF为正方形，所以ED⊥CD

因为二面角E﹣DC﹣A的大小为90°，所以平面EDCF⊥平面ABCD，

由面面垂直的性质定理得ED⊥平面ABCD，又AD平面ABCD，

所以ED⊥AD，又因为∠ADC＝120°，AB∥CD，

所以∠DAB＝60°，又AB＝2AD＝2，

所以由余弦定理得BD，所以AD2+BD2＝AB2，即AD⊥BD，

又DE∩DB＝D，DE，DB平面BDE，所以AD⊥平面BDE；

（2）设点D到平面ABE的距离为h，则VE﹣ABD＝VD﹣ABE，

所以所以h，

所以点D到平面ABE的距离为．