题目内容
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,
时,![]() ,求证:
,求证:![]() .
.
【答案】(1) 见解析;(2)证明见解析
【解析】
(1)由f(x)含有参数a,单调性和a的取值有关,通过分类讨论说明导函数的正负,进而得到结论;
(2)法一:将已知变形,对a分类讨论研究![]() 的正负,当
的正负,当![]() 与
与![]() 时,通过单调性可直接说明,当
时,通过单调性可直接说明,当![]() 时,可得g(x)的最大值为
时,可得g(x)的最大值为![]() ,利用导数解得结论.
,利用导数解得结论.
法二:分析![]() 时,
时,![]() 且
且![]() 使得已知不成立;当
使得已知不成立;当![]() 时,利用分离变量法求解证明.
时,利用分离变量法求解证明.
(1)![]() ,
,
①当![]() 时,由
时,由![]() 得
得![]() ,得
,得![]() ,所以
,所以![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 时,由
时,由![]() 得
得![]() ,解得
,解得![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 在
在![]() 上单调递减;
上单调递减;
(2)法一:由![]() 得
得![]() (*),
(*),
设![]() ,则
,则![]() ,
,
①当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,可知
,可知![]() 且
且![]() 时,
时,
![]() ,
,![]() ,可知(*)式不成立;
,可知(*)式不成立;
②当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,可知(*)式成立;
,可知(*)式成立;
③当![]() 时,由
时,由![]() 得
得![]() ,
,
所以![]() 在
在![]() 上单调递增,可知
上单调递增,可知![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,由(*)式得
,由(*)式得![]() ,
,
设![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递减,而
上单调递减,而![]() ,h(1)=1-2=-1<0,
,h(1)=1-2=-1<0,
所以存在t![]() ,使得h(t)=0,由
,使得h(t)=0,由![]() 得
得![]() ;
;
综上所述,可知![]() .
.
法二:由![]() 得
得![]() (*),
(*),
①当![]() 时,得
时,得![]() ,
,![]() 且
且![]() 时,
时,
![]() ,可知(*)式不成立;
,可知(*)式不成立;
②当![]() 时,由(*)式得
时,由(*)式得![]() ,即
,即![]() ,
,
设![]() ,则
,则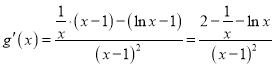 ,
,
设![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
又![]() ,
,![]() ,所以
,所以![]() ,
,![]() (**),
(**),
当![]() 时,
时,![]() ,得
,得![]() ,所以
,所以![]() 在
在![]() 上递增,
上递增,
同理可知![]() 在
在![]() 上递减,所以
上递减,所以![]() ,
,
结合(**)式得![]() ,所以
,所以![]() ,
,
综上所述,可知![]() .
.

练习册系列答案
相关题目