题目内容
【题目】在平面直角坐标系xOy中,已知点A,B的坐标分别为(﹣2,0),(2,0).直线AP,BP相交于点P,且它们的斜率之积是﹣ ![]() .记点P的轨迹为Г. (Ⅰ)求Г的方程;
.记点P的轨迹为Г. (Ⅰ)求Г的方程;
(Ⅱ)已知直线AP,BP分别交直线l:x=4于点M,N,轨迹Г在点P处的切线与线段MN交于点Q,求 ![]() 的值.
的值.
【答案】解:(Ⅰ)设点P坐标为(x,y),则 直线AP的斜率 ![]() (x≠﹣2);
(x≠﹣2);
直线BP的斜率 ![]() (x≠2).
(x≠2).
由已知有 ![]() (x≠±2),
(x≠±2),
化简得点P的轨迹Г的方程为 ![]() (x≠±2).
(x≠±2).
(Ⅱ)设P(x1 , y1)(x1≠±2),则 ![]() .
.
直线AP的方程为 ![]() ,令x=4,得点M纵坐标为
,令x=4,得点M纵坐标为 ![]() ;
;
直线BP的方程为 ![]() ,令x=4,得点N纵坐标为
,令x=4,得点N纵坐标为 ![]() ;
;
设在点P处的切线方程为y﹣y1=k(x﹣x1),
由 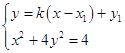 ,得
,得 ![]() .
.
由△=0,得 ![]() =0,
=0,
整理得 ![]() .
.
将 ![]() 代入上式并整理得:
代入上式并整理得: ![]() ,解得
,解得 ![]() ,
,
∴切线方程为 ![]() .
.
令x=4得,点Q纵坐标为 ![]() =
= ![]() .
.
设 ![]() ,则yQ﹣yM=λ(yN﹣yQ),
,则yQ﹣yM=λ(yN﹣yQ),
∴ 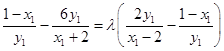 .
.
∴ 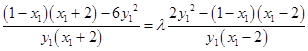 .
.
将 ![]() 代入上式,得
代入上式,得 ![]() ,
,
解得λ=1,即 ![]() =1.
=1.
【解析】(Ⅰ)设出P点坐标,求得AP、BP所在直线的斜率,由斜率之积是﹣ ![]() 列式整理即可得到Г的方程;(Ⅱ)设出P点坐标,得到AP、BP的方程,进一步求出M、N的纵坐标,再写出椭圆在P点的切线方程,由判别式等于0得到过P的斜率(用P的坐标表示),再代入切线方程,求得Q点纵坐标,设
列式整理即可得到Г的方程;(Ⅱ)设出P点坐标,得到AP、BP的方程,进一步求出M、N的纵坐标,再写出椭圆在P点的切线方程,由判别式等于0得到过P的斜率(用P的坐标表示),再代入切线方程,求得Q点纵坐标,设 ![]() ,转化为坐标的关系即可求得λ,从而得到
,转化为坐标的关系即可求得λ,从而得到 ![]() 的值.
的值.
【考点精析】关于本题考查的椭圆的标准方程,需要了解椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能得出正确答案.
才能得出正确答案.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
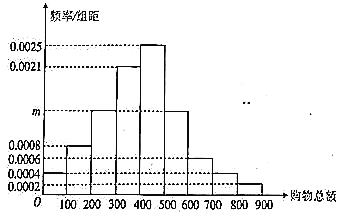
冲刺100分单元优化练考卷系列答案【题目】某商场销售某种品牌的空调器,每周周初购进一定数量的空调器,商场每销售一台空调器可获利500元,若供大于求,则每台多余的空调器需交保管费100元;若供不应求,则可从其他商店调剂供应,此时每台空调器仅获利润200元. (Ⅰ)若该商场周初购进20台空调器,求当周的利润(单位:元)关于当周需求量n(单位:台,n∈N)的函数解析式f(n);
(Ⅱ)该商场记录了去年夏天(共10周)空调器需求量n(单位:台),整理得表:
周需求量n | 18 | 19 | 20 | 21 | 22 |
频数 | 1 | 2 | 3 | 3 | 1 |
以10周记录的各需求量的频率作为各需求量发生的概率,若商场周初购进20台空调器,X表示当周的利润(单位:元),求X的分布列及数学期望.