��Ŀ����
����Ŀ��ij�����̳�Ϊ���˽�˿͵Ĺ�����Ϣ,������̳��ռ���![]() λ�˿͵Ĺ����ܶ�(��λԪ),�����ݰ���
λ�˿͵Ĺ����ܶ�(��λԪ),�����ݰ���![]()
![]() ��
��![]()
![]() �ֳ�
�ֳ�![]() ��,�Ƴ�������ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ:
��,�Ƴ�������ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ:
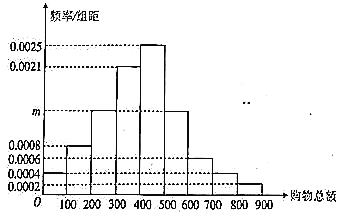
���̳�ÿ�մ�Լ��![]() ���˿�,Ϊ�������̳������ܶ�,���ڶ�һ���Թ��ﲻ����
���˿�,Ϊ�������̳������ܶ�,���ڶ�һ���Թ��ﲻ����![]() Ԫ�Ĺ˿ͷ��ż���Ʒ.
Ԫ�Ĺ˿ͷ��ż���Ʒ.
(1)��Ƶ�ʷֲ�ֱ��ͼ��![]() ��ֵ,������ÿ��Ӧ������Ʒ��������
��ֵ,������ÿ��Ӧ������Ʒ��������
(2)��ÿ�հ��ֲ�����ķ����ӹ����ܶ���![]() �����Ӧ�Ĺ˿��г�ȡ
�����Ӧ�Ĺ˿��г�ȡ![]() ���˿�,��
���˿�,��![]() ���˿����������ȡ���������˿�,ÿ�˽���һ���������,���ó���������������Բ�ͬ��ĸ���.
���˿����������ȡ���������˿�,ÿ�˽���һ���������,���ó���������������Բ�ͬ��ĸ���.
���𰸡���1��![]() ,3650��2��
,3650��2��![]()
��������������(1)����Ƶ�ʷֲ�ֱ��ͼ�У�����С�������֮��Ϊ1�����ʣ��������m��ֵ������Ƶ�ʷֲ�ֱ��ͼ������������ﳬ��300Ԫ�˿͵�Ƶ�ʣ����ݸ��ʼ���������������Ʒ��������
(2) ���ݷֲ������ÿ�����屻���еĸ�����ȣ��ڳ���600Ԫ�Ĺ˿��й���ȡ6��������Ƶ�ʷֲ�ֱ��ͼ�ɵõ����������ֱ�Ϊ3,2,1�������оٷ��оٳ����п��ܣ����ҳ����������Բ�ͬ������������������������Բ�ͬ��ĸ��ʡ�
���: ![]() (1)
(1) ![]()
![]()
![]() ��
��![]()
![]() .
.
���̳�ÿ��Ӧ������Ʒ��������ԼΪ![]()
![]() .
.
(2)��ֱ��ͼ��֪![]() ������������Ϊ
������������Ϊ![]() ,�����������ȡ�������ֱ�Ϊ
,�����������ȡ�������ֱ�Ϊ![]() .
.
����![]() �˷ֱ�Ϊ
�˷ֱ�Ϊ![]() ,
,![]() .���г�ȡ�����
.���г�ȡ�����![]()
![]() ��
��
![]() ��
��![]()
![]() ��15��.
��15��.
�����������Բ�ͬ����![]() ��,���Ի�ó���������������Բ�ͬ��ĸ���Ϊ
��,���Ի�ó���������������Բ�ͬ��ĸ���Ϊ![]() .
.

 ��У����ϵ�д�
��У����ϵ�д�