题目内容
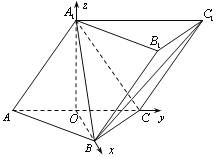
【题目】如图,在三棱柱![]() 中,侧面
中,侧面![]() 底面ABC,
底面ABC,![]()
![]() ,且
,且![]() ,O为AC中点.
,O为AC中点.

(1)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)在![]() 上是否存在一点E,使得
上是否存在一点E,使得![]() 平面
平面![]() ,若不存在,说明理由;若存在,确定点E的位置.
,若不存在,说明理由;若存在,确定点E的位置.
【答案】(1)![]() .;(2)E为
.;(2)E为![]() 的中点.
的中点.
【解析】
(1)由已知中![]() ,O为AC中点,根据等腰三角形“三线合一”的性质,可得
,O为AC中点,根据等腰三角形“三线合一”的性质,可得![]() ,又由已知中侧面
,又由已知中侧面![]() 底面ABC,故
底面ABC,故![]() 平面ABC,以O为原点,OB,OC,
平面ABC,以O为原点,OB,OC,![]() 所在直线分别为x,y,z轴建立空间直角坐标系,分别求出直线
所在直线分别为x,y,z轴建立空间直角坐标系,分别求出直线![]() 的方向向量与平面
的方向向量与平面![]() 的法向量,代入空间向量夹角公式,即可得到直线
的法向量,代入空间向量夹角公式,即可得到直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)设出E点的坐标,根据![]() 平面
平面![]() ,则OE的方向向量与平面
,则OE的方向向量与平面![]() 的法向量垂直,数量积为零,我们可以求出E点坐标,进而确定E点的位置.
的法向量垂直,数量积为零,我们可以求出E点坐标,进而确定E点的位置.
(1)如图,因为![]() ,且O为AC的中点,所以
,且O为AC的中点,所以![]() 平面
平面![]() 平面
平面![]() ,交线为
,交线为![]() ,且
,且![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
以O为原点,![]() 所在直线分别为x,y,z轴建立空间直角坐标系.由题意可知,
所在直线分别为x,y,z轴建立空间直角坐标系.由题意可知,![]() 又
又![]()
![]()
所以得:![]()
则有:![]()
设平面![]() 的一个法向量为
的一个法向量为![]() ,则有
,则有
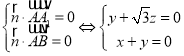 ,
,
令![]() ,得
,得![]()
所以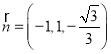 .
.
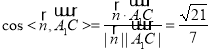
因为直线![]() 与平面
与平面![]() 所成角
所成角![]() 和向量
和向量![]() 与
与![]() 所成锐角互余,
所成锐角互余,
所以![]() .
.
(2)设![]()
即![]() ,得
,得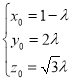
所以![]() 得
得![]()
令![]() 平面
平面![]() ,得
,得![]() ,
,
即![]() 得
得![]() 即存在这样的点E,E为
即存在这样的点E,E为![]() 的中点.
的中点.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
【题目】某高校在2017年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如表:
组号 | 分组 | 频率 |
第1组 |
|
|
第2组 |
|
|
第3组 |
|
|
第4组 |
|
|
第5组 |
|
|

![]() 求出频率分布表中
求出频率分布表中![]() 处应填写的数据,并完成如图所示的频率分布直方图;
处应填写的数据,并完成如图所示的频率分布直方图;
![]() 根据直方图估计这次自主招生考试笔试成绩的平均数和中位数
根据直方图估计这次自主招生考试笔试成绩的平均数和中位数![]() 结果都保留两位小数
结果都保留两位小数![]() .
.