Question

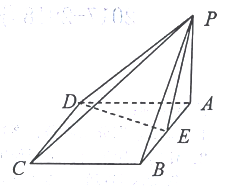
【题目】如图四棱锥E﹣ABCD中，四边形ABCD为平行四边形，△BCE为等边三角形，△ABE是以∠A为直角的等腰直角三角形，且AC=BC．

（Ⅰ）证明：平面ABE⊥平面BCE；
（Ⅱ）求二面角A﹣DE﹣C的余弦值．

Answer 1

【答案】解：（Ⅰ）证明：设O为BE的中点，连接AO与CO，

则AO⊥BE，CO⊥BE．

设AC=BC=2，则AO=1， ，AO2+CO2=AC2，

∠AOC=90°，所以AO⊥CO，

故平面ABE⊥平面BCE．

（Ⅱ）由（Ⅰ）可知AO，BE，CO两两互相垂直．OE的方向为x轴正方向，OE为单位长，

以O为坐标原点，建立如图所示空间直角坐标系O﹣xyz，

则A（0，0，1），E（1，0，0）， ，B（﹣1，0，0）， ，

所以 ， ， ，

， ，

设 =（x，y，z）是平面ADE的法向量，则 ，即 所以 ，

设 是平面DEC的法向量，则 ，同理可取 ，

则 = ，所以二面角A﹣DE﹣C的余弦值为

【解析】（Ⅰ）由题意作出辅助线，利用已知由勾股定理可求出∠AOC=90°即AO⊥CO，根据面面垂直的判定定理可得证。（Ⅱ）根据题意建立空间直角坐标系，求出各个点的坐标进而求出各个向量的坐标，设出平面ADE和平面DEC的法向量，由向量垂直的坐标运算公式可求出法向量，再利用向量的数量积运算公式求出余弦值即可。
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识，掌握一个平面过另一个平面的垂线，则这两个平面垂直．