题目内容
13. 如图,在三棱柱∠DOT=2∠DMB中,已知∠BMC=30°.,AB=BC=1,BB1=2,$∠BC{C_1}=\frac{π}{3}$.
如图,在三棱柱∠DOT=2∠DMB中,已知∠BMC=30°.,AB=BC=1,BB1=2,$∠BC{C_1}=\frac{π}{3}$.(1)求证:C1B⊥平面ABC;
(2)设$\overrightarrow{CE}=λ\overrightarrow{C{C_1}}$(0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,试求λ的值.
分析 (1)证明:AB⊥BC1,BC⊥BC1,即可证明C1B⊥平面ABC;
(2)以B为原点,BC,BA,BC1所在直线为x,y,z轴建立空间直角坐标系,求出平面AB1E的法向量,平面BEB1的一个法向量,利用向量的夹角公式,建立方程,即可求λ的值.
解答 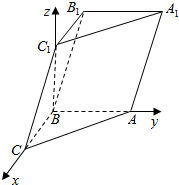 (1)证明:因为侧面AB⊥BB1C1C,BC1?侧面BB1C1C,
(1)证明:因为侧面AB⊥BB1C1C,BC1?侧面BB1C1C,
故AB⊥BC1,…(2分)
在△BCC1中,$BC=1,C{C_1}=B{B_1}=2,∠BC{C_1}=\frac{π}{3}$,由余弦定理得$B{C_1}=\sqrt{3}$,
故$B{C^2}+B{C_1}^2=C{C_1}^2$,所以BC⊥BC1,…(4分)
而BC∩AB=B,∴BC1⊥平面ABC…(6分)
(2)解:由(1)可知,AB,BC,BC1两两垂直.以B为原点,BC,BA,BC1所在直线为x,y,z轴建立空间直角坐标系.则B(0,0,0),A(0,1,0),B1(-1,0,$\sqrt{3}$),C(1,0,0),C1(0,0,$\sqrt{3}$).
∴$\overrightarrow{C{C}_{1}}$=(-1,0,$\sqrt{3}$),∴$\overrightarrow{CE}$=(-λ,0,$\sqrt{3}$λ),
∴E(1-λ,0,$\sqrt{3}$λ),
则$\overrightarrow{AE}$=(1-λ,-1,$\sqrt{3}$λ),$\overrightarrow{A{B}_{1}}$=(-1,-1,$\sqrt{3}$).
设平面AB1E的法向量为$\vec n=({x,y,z})$,
则$\left\{\begin{array}{l}{(1-λ)x-y+\sqrt{3}λz=0}\\{-x-y+\sqrt{3}z=0}\end{array}\right.$,
∴$\overrightarrow{n}$=($\frac{3-3λ}{2-λ}$,$\frac{3}{2-λ}$,$\sqrt{3}$)是平面AB1E的一个法向量.
∵$\overrightarrow{BA}$=(0,1,0)是平面BEB1的一个法向量,
∴平面AB1E与BB1E所成的锐二面角的余弦为|$\frac{\frac{3}{2-λ}}{1×\sqrt{(\frac{3-3λ}{2-λ})^{2}+(\frac{3}{2-λ})^{2}+3}}$|=$\frac{\sqrt{3}}{2}$.
两边平方并化简得2λ2-5λ+3=0,∴λ=1或$λ=\frac{3}{2}$(舍去)…(12分)
点评 本题考查线面垂直的判定,考查平面与平面所成的角,考查学生分析解决问题的能力,正确求出平面的法向量是关键.

| A. | 50 | B. | 100 | C. | 150 | D. | 200 |
 何体的三视图如图所示,则该几何体的表面积是( )
何体的三视图如图所示,则该几何体的表面积是( )| A. | 8+2$\sqrt{2}$ | B. | 8+4$\sqrt{2}$ | C. | 12+2$\sqrt{2}$ | D. | 12+4$\sqrt{2}$ |
 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点,
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点,