题目内容
9.已知椭圆的焦点为(-1,0)和(1,0).点P(2,0)在椭圆上,则椭圆的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1.分析 设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),由题意可得c=1,a=2,再由a,b,c的关系,可得b,进而得到椭圆方程.
解答 解:设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
由题意可得c=1,a=2,
b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{4-1}$=$\sqrt{3}$,
即有椭圆方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1.
故答案为:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1.
点评 本题考查椭圆的方程的求法,注意运用待定系数法,考查椭圆的焦点的运用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.下列说法正确的是( )
| A. | 铺的很平的一张白纸是一个平面 | B. | 平面是矩形或平行四边形的形状 | ||
| C. | 两个平面叠在一起比一个平面厚 | D. | 平面的直观图一般画成平行四边形 |
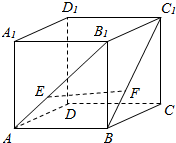 如图,正方体ABCD-A1B1C1D1,E,F分别在AB1,BC1上,且$\frac{{B}_{1}E}{AE}$=$\frac{{C}_{1}F}{BF}$=2,过EF做一个平面和面ABCD相交,并找到交线,写出作法.(注意:交线必须是由两个确定的点的连线)
如图,正方体ABCD-A1B1C1D1,E,F分别在AB1,BC1上,且$\frac{{B}_{1}E}{AE}$=$\frac{{C}_{1}F}{BF}$=2,过EF做一个平面和面ABCD相交,并找到交线,写出作法.(注意:交线必须是由两个确定的点的连线)