题目内容
如图所示,等边△ABC的边长为4,D为BC中点,沿AD把△ADC折叠到△ADC′处,
使二面角B-AD-C′为60°,则折叠后二面角A-BC′-D的正切值为________.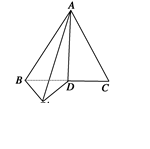
使二面角B-AD-C′为60°,则折叠后二面角A-BC′-D的正切值为________.

2
由二面角的平面角的概念可知:∠BDC/即为二面角B-AD-C′的平面角,有∠BDC/=60°,所以BC/=2,作DM⊥BC′于点M,连接AM,则AM为点A到直线BC′的距离,二面角A-BC′-D的平面角即为∠AMD.
如图,作DM⊥BC′于点M,连接AM,则AM为点A到直线BC′的距离, AD=2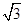 ,DM=
,DM=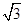 ,所以AM=
,所以AM=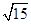 ,然后利用三角函数的正切值得到结论为2.
,然后利用三角函数的正切值得到结论为2.
如图,作DM⊥BC′于点M,连接AM,则AM为点A到直线BC′的距离, AD=2
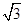 ,DM=
,DM=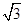 ,所以AM=
,所以AM=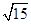 ,然后利用三角函数的正切值得到结论为2.
,然后利用三角函数的正切值得到结论为2.
练习册系列答案
相关题目
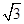 ,E、F分别为AB、CD中点,且EF=4,则AD与BC所成的角是 .
,E、F分别为AB、CD中点,且EF=4,则AD与BC所成的角是 . 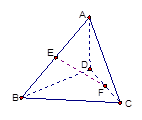
 ,BC=CC1=1,则异面直线AC1与BB1所成的角的大小为( )
,BC=CC1=1,则异面直线AC1与BB1所成的角的大小为( )

 中,底面正方形
中,底面正方形 的边长为1,侧棱长为2,则异面直线
的边长为1,侧棱长为2,则异面直线 与
与 所成角的大小为( )
所成角的大小为( )



 中,
中, ,E、F分别为
,E、F分别为 和AD的中点,则异面直线
和AD的中点,则异面直线 、EF所成的角为( )
、EF所成的角为( )



 中,若
中,若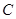 为直角,则有
为直角,则有 ;类比到三棱锥
;类比到三棱锥 中,若三个侧面
中,若三个侧面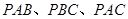 两两垂直,且分别与底面所成的角为
两两垂直,且分别与底面所成的角为 ,则有
,则有 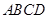 -
- 中,
中, 为
为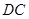 的中点,则
的中点,则 与
与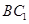 所在直线所成角的余弦值等于 ( ) ( )
所在直线所成角的余弦值等于 ( ) ( )



