题目内容
12.如图,在长方体ABCD-A1B1C1D1中,E是棱BC的中点,过BD1的一个平面与平面DEC1交于MN.求证:BD1∥MN.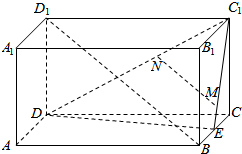
分析 连接D1C与DC1,交于点F,由中位线定理得EF∥BD1,从而得到BD1∥平面BEC1,由此能证明BD1∥MN.
解答  解:连接D1C与DC1,交于点F,则F是DC1的中点,连接EF,
解:连接D1C与DC1,交于点F,则F是DC1的中点,连接EF,
∵E是BC中点,∴由中位线定理得EF∥BD1,
∵BD1?平面DEC1,EF?平面DEC1,
∴BD1∥平面BEC1,
∵过BD1的一个平面与平面DEC1交于MN,
∴BD1与MN共面,
∴BD1∥MN.
点评 本题考查两直线平行的证明,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
17.若sin3θ-cos3θ≥sinθ-cosθ,0<θ<2π,则角θ的取值范围是( )
| A. | [$\frac{π}{2}$,π]∪[$\frac{3π}{2}$,2π) | B. | [$\frac{π}{4}$,$\frac{π}{2}$]∪[π,$\frac{5π}{4}$]∪[$\frac{3π}{2}$,2π) | ||
| C. | [$\frac{π}{4}$,π]∪[$\frac{5π}{4}$,2π) | D. | [$\frac{π}{4}$,$\frac{π}{2}$]∪[$\frac{5π}{4}$,$\frac{3π}{2}$]∪[$\frac{7π}{4}$,2π) |
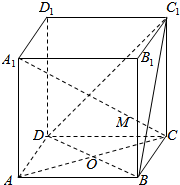 已知在正方体ABCD-A1B1C1D1中,O是DB的中点,直线A1C交平面C1BD于点M,判断下列结论是否正确:
已知在正方体ABCD-A1B1C1D1中,O是DB的中点,直线A1C交平面C1BD于点M,判断下列结论是否正确: