题目内容
已知数列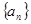 的前n项和为
的前n项和为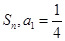 且
且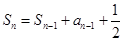 ,数列
,数列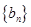 满足
满足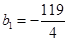 且
且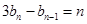
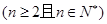 .
.
(1)求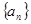 的通项公式;
的通项公式;
(2)求证:数列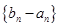 为等比数列;
为等比数列;
(3)求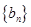 前n项和.
前n项和.
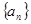 的前n项和为
的前n项和为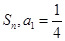 且
且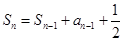 ,数列
,数列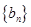 满足
满足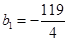 且
且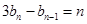
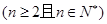 .
.(1)求
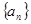 的通项公式;
的通项公式;(2)求证:数列
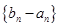 为等比数列;
为等比数列;(3)求
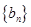 前n项和.
前n项和.(1)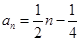 ;(2)见解析;(3)
;(2)见解析;(3)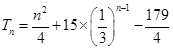 .
.
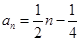 ;(2)见解析;(3)
;(2)见解析;(3)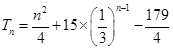 .
.试题分析:(1)利用
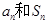 的关系得到
的关系得到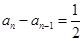 ,可见
,可见 为等差数列;(2)利用等比数列定义证明即可;(3)写出
为等差数列;(2)利用等比数列定义证明即可;(3)写出 通项公式,然后分组求和,注意
通项公式,然后分组求和,注意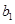 在特殊位置.
在特殊位置.试题解析:(1)由
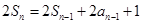 得
得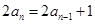 ,
, 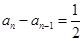
∴
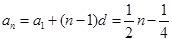
(2)∵
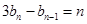 ,∴
,∴ ,
,∴
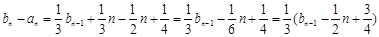 ;
; ,∴由上面两式得
,∴由上面两式得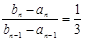 ,又
,又 。∴数列
。∴数列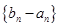 是以-30为首项,
是以-30为首项, 为公比的等比数列.
为公比的等比数列. (3)由(2)得
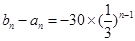 ,∴
,∴
 前n项和
前n项和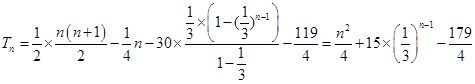 .
.
练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
 满足
满足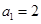 ,
,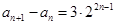
 ,求数列
,求数列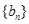 的前
的前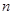 项和
项和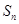 .
.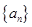 的公差
的公差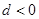 ,若
,若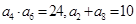 ,则该数列的前
,则该数列的前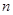 项和
项和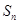 的最大值是( )
的最大值是( )
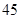
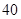
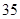
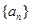 中,
中,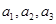 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且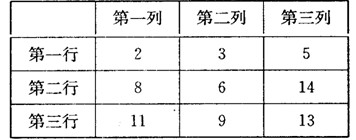
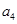 的值为( )
的值为( )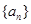 的前
的前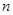 项和为
项和为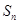 .若
.若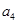 是
是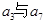 的等比中项,
的等比中项, 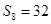 ,则
,则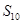 =( ).
=( ). 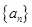 的公差
的公差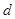 ≠0,
≠0,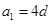 .若
.若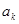 是
是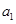 与
与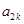 的等比中项,则
的等比中项,则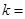 ( )
( )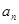 }满足
}满足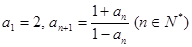 ,则
,则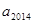 的值为 .
的值为 .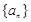 中,若
中,若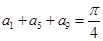 ,则
,则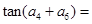 _________________.
_________________.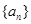 的前
的前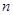 项和为
项和为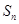 ,若
,若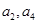 是方程
是方程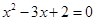 的两个实数根,则
的两个实数根,则 .
.