题目内容
已知函数 的最小值为0,其中
的最小值为0,其中
(Ⅰ)求 的值;
的值;
(Ⅱ)若对任意的 有
有 ≤
≤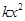 成立,求实数
成立,求实数 的最小值;
的最小值;
(Ⅲ)证明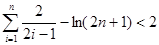 (
( ).
).
 的最小值为0,其中
的最小值为0,其中
(Ⅰ)求
 的值;
的值;(Ⅱ)若对任意的
 有
有 ≤
≤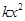 成立,求实数
成立,求实数 的最小值;
的最小值;(Ⅲ)证明
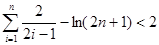 (
( ).
).(1) 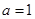 (2)
(2) 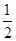 (3) 见解析
(3) 见解析
【考点定位】本小题主要考查导数的运算,利用导数研究函数的单调性,不等式基础知识.考查函数思想、分类讨论思想.考查综合分析和解决问题的能力.试题分为三问,题面比较简单,给出的函数比较常规,因此入手对于同学们来说没有难度,第二问中,解含参数的不等式时,要注意题中参数的讨论所有的限制条件,从而做到不重不漏;第三问中,证明不等式,应借助于导数证不等式的方法进行.
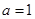 (2)
(2) 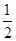 (3) 见解析
(3) 见解析【考点定位】本小题主要考查导数的运算,利用导数研究函数的单调性,不等式基础知识.考查函数思想、分类讨论思想.考查综合分析和解决问题的能力.试题分为三问,题面比较简单,给出的函数比较常规,因此入手对于同学们来说没有难度,第二问中,解含参数的不等式时,要注意题中参数的讨论所有的限制条件,从而做到不重不漏;第三问中,证明不等式,应借助于导数证不等式的方法进行.
(1)解:  的定义域为
的定义域为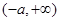
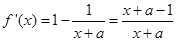
由 ,得
,得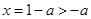
当x变化时,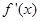 ,
, 的变化情况如下表:
的变化情况如下表:
因此, 在
在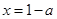 处取得最小值,故由题意
处取得最小值,故由题意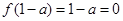 ,所以
,所以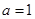
(2)解:当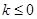 时,取
时,取 ,有
,有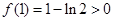 ,故
,故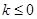 时不合题意.当
时不合题意.当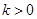 时,令
时,令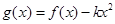 ,即
,即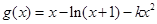
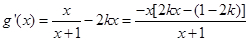
令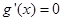 ,得
,得
①当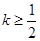 时,
时,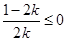 ,
,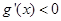 在
在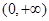 上恒成立。因此
上恒成立。因此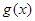 在
在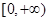 上单调递减.从而对于任意的
上单调递减.从而对于任意的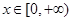 ,总有
,总有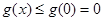 ,即
,即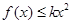 在
在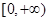 上恒成立,故
上恒成立,故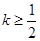 符合题意.
符合题意.
②当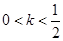 时,
时,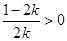 ,对于
,对于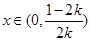 ,
, ,故
,故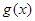 在
在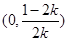 上单调递增.因此当取
上单调递增.因此当取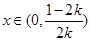 时,
时,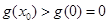 ,即
,即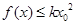 不成立.
不成立.
故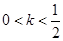 不合题意.
不合题意.
综上,k的最小值为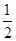 .
.
(3)证明:当n=1时,不等式左边=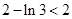 =右边,所以不等式成立.
=右边,所以不等式成立.
当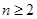 时,
时,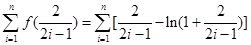
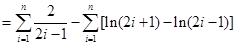
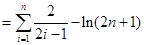
在(2)中取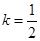 ,得
,得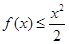
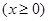 ,
,
从而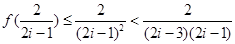
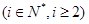
所以有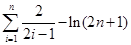
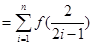
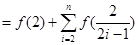
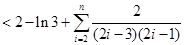
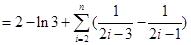
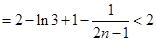
综上,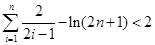 ,
,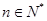
 的定义域为
的定义域为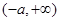
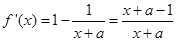
由
 ,得
,得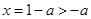
当x变化时,
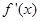 ,
, 的变化情况如下表:
的变化情况如下表:| x | 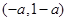 | 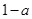 | 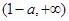 |
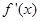 | - | 0 | + |
 | 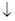 | 极小值 | 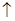 |
 在
在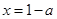 处取得最小值,故由题意
处取得最小值,故由题意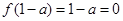 ,所以
,所以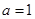
(2)解:当
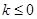 时,取
时,取 ,有
,有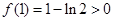 ,故
,故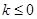 时不合题意.当
时不合题意.当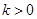 时,令
时,令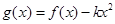 ,即
,即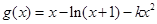
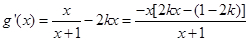
令
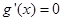 ,得
,得
①当
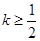 时,
时,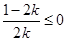 ,
,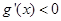 在
在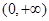 上恒成立。因此
上恒成立。因此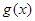 在
在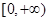 上单调递减.从而对于任意的
上单调递减.从而对于任意的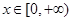 ,总有
,总有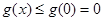 ,即
,即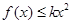 在
在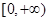 上恒成立,故
上恒成立,故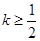 符合题意.
符合题意.②当
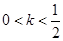 时,
时,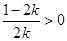 ,对于
,对于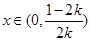 ,
, ,故
,故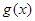 在
在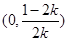 上单调递增.因此当取
上单调递增.因此当取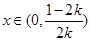 时,
时,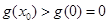 ,即
,即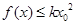 不成立.
不成立.故
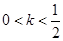 不合题意.
不合题意.综上,k的最小值为
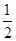 .
.(3)证明:当n=1时,不等式左边=
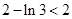 =右边,所以不等式成立.
=右边,所以不等式成立.当
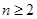 时,
时,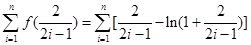
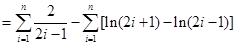
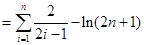
在(2)中取
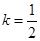 ,得
,得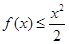
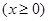 ,
,从而
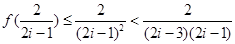
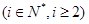
所以有
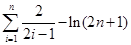
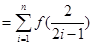
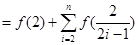
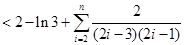
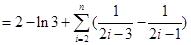
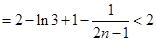
综上,
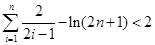 ,
,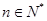

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 的图象按向量
的图象按向量 平移得到函数
平移得到函数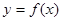 的图象.
的图象.  ,证明:
,证明: .
. 的最大值和最小值分别为
的最大值和最小值分别为
 ,
,


 是定义在
是定义在 上的函数,其图象是一条连续的曲线,且满足下列条件:①
上的函数,其图象是一条连续的曲线,且满足下列条件:① ,
, ∈
∈ |<|
|<| 立方米时,只付基本费9元和每户每月定额损耗费
立方米时,只付基本费9元和每户每月定额损耗费 元;
元; 元的超额费;
元的超额费; (元)与月用水量
(元)与月用水量 (立方米)的函数关系式;
(立方米)的函数关系式; 的值。
的值。 ,其长为32米,宽为18米,现要在此空地上种植一块矩形草坪,三边留有人行道,人行道宽度为
,其长为32米,宽为18米,现要在此空地上种植一块矩形草坪,三边留有人行道,人行道宽度为 米与
米与 米均不小于2米,且要求“转角处”(图中矩形
米均不小于2米,且要求“转角处”(图中矩形 )的面积为8平方米
)的面积为8平方米 ,并指出
,并指出
 ,
, ,且
,且 ;
; ;
; 时,
时,
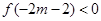 恒成立,求实数
恒成立,求实数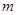 的取值范围。
的取值范围。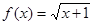 则
则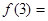
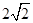
 ,那么
,那么