题目内容
(本小题满分12分)某射击运动员在一次射击中,命中10环、9环、8环、7环的概率分别为0.2、0.35、0.2、0.15。求此运动员
(1)在一次射击中,命中10环或9环的概率。
(2)在一次射击中,命中环数小于8环的概率。
(3)在两次射击中,至少有一次击中10环的概率。
(1)在一次射击中,命中10环或9环的概率。
(2)在一次射击中,命中环数小于8环的概率。
(3)在两次射击中,至少有一次击中10环的概率。
(1)0.55
(2)0.25
(3)0.36
(1)设“命中10环”与“命中9环”分别为事件A与B,则A、B互斥,
故P(A+B)=P(A)+P(B)=0.2+0.35=0.55………………………………(4分)
(2)设“命中10环、9环或8环”为事件C,则P(C)=0.2+0.35+0.2=0.75
故小于8环的概率:P(
 )=1-P(C)=0.25………………………………(8分)
)=1-P(C)=0.25………………………………(8分)(3)设“第一次命中10环”与“第二次命中10环”分别为事件A、B,则A与B相互独立,则至少有一次击中10环的概率为
P=1-P(
 )·P(
)·P(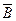 )=1-0.82=0.36…………………………………………(12分)
)=1-0.82=0.36…………………………………………(12分)
练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目

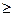 245 ,z
245 ,z 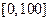 上是等可能出现的.单项80分以上,且总分170分以上才合格,求他合格的概率。
上是等可能出现的.单项80分以上,且总分170分以上才合格,求他合格的概率。 均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次, 两次点数和较大的当选志愿者. 甲先抛掷两次,第1次向上点数为3,第2次向上
均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次, 两次点数和较大的当选志愿者. 甲先抛掷两次,第1次向上点数为3,第2次向上 点数为4.
点数为4. 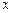 ,第二次出现的点数为
,第二次出现的点数为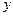 ,用
,用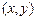 表示
表示 先后
先后 抛掷两次的结果,试写出两次向上点数和与甲相同的所有可能结果.
抛掷两次的结果,试写出两次向上点数和与甲相同的所有可能结果. 形的顶点为圆心,半径为1的圆弧,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则它击中阴影部分的概率是 .
形的顶点为圆心,半径为1的圆弧,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则它击中阴影部分的概率是 . 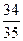
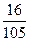
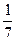
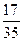
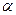 “第一次被抽到的概率”“第二次被抽到的概率”“在整个抽样过程中被抽到的概率”分别是
“第一次被抽到的概率”“第二次被抽到的概率”“在整个抽样过程中被抽到的概率”分别是 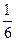 ,
,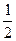
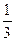
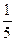 ,
,