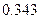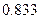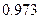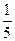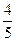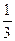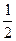题目内容
(9分)甲、乙两位同学报名参加2010年在广州举办的亚运会志愿者服务,两人条件相当,但名额只有一人. 两人商量采用抛骰子比大小的方法决定谁去,每人将一颗质地 均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次, 两次点数和较大的当选志愿者. 甲先抛掷两次,第1次向上点数为3,第2次向上
均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次, 两次点数和较大的当选志愿者. 甲先抛掷两次,第1次向上点数为3,第2次向上 点数为4.
点数为4.
(1)记乙第一次出现的点数为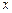 ,第二次出现的点数为
,第二次出现的点数为 ,用
,用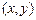 表示
表示 先后
先后 抛掷两次的结果,试写出两次向上点数和与甲相同的所有可能结果.
抛掷两次的结果,试写出两次向上点数和与甲相同的所有可能结果.
(2)求乙抛掷两次后,向上点数和与甲相同的概率?
(3)求乙抛掷两次后,能决定乙当选志愿者的概率?
 均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次, 两次点数和较大的当选志愿者. 甲先抛掷两次,第1次向上点数为3,第2次向上
均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次, 两次点数和较大的当选志愿者. 甲先抛掷两次,第1次向上点数为3,第2次向上 点数为4.
点数为4. (1)记乙第一次出现的点数为
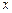 ,第二次出现的点数为
,第二次出现的点数为 ,用
,用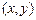 表示
表示 先后
先后 抛掷两次的结果,试写出两次向上点数和与甲相同的所有可能结果.
抛掷两次的结果,试写出两次向上点数和与甲相同的所有可能结果.(2)求乙抛掷两次后,向上点数和与甲相同的概率?
(3)求乙抛掷两次后,能决定乙当选志愿者的概率?
(1)(1)乙两次向上点数和与甲相同,即乙两次向上点数和为7,所有可能结果有:
 .
.
(2)向上点数和与甲相同的概率为 .
.
(3) 能决定乙当选志愿者的概率为
能决定乙当选志愿者的概率为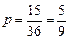 .
.
 .
.(2)向上点数和与甲相同的概率为
 .
.(3)
 能决定乙当选志愿者的概率为
能决定乙当选志愿者的概率为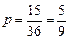 .
.解:(1)乙两次向上点数和与甲相同,即乙两次向上点数和为7,所有可能结果有:
 . ……
. …… (2
(2 分)
分)
(2)乙抛掷两次后,共有 种结果,而向上点数和
种结果,而向上点数和 为7的结果有6种,
为7的结果有6种, 所以向上点数和与甲相同的概率为
所以向上点数和与甲相同的概率为 . ……(5分)
. ……(5分)
(3)若乙当选志愿者,则向上点数和应大于7,所有可能结果有:
 ,
,
共15种,所以 能决定乙当选志愿者的概率为
能决定乙当选志愿者的概率为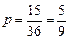 . ……(9分)
. ……(9分)
 . ……
. …… (2
(2 分)
分)(2)乙抛掷两次后,共有
 种结果,而向上点数和
种结果,而向上点数和 为7的结果有6种,
为7的结果有6种, 所以向上点数和与甲相同的概率为
所以向上点数和与甲相同的概率为 . ……(5分)
. ……(5分)(3)若乙当选志愿者,则向上点数和应大于7,所有可能结果有:
 ,
,共15种,所以
 能决定乙当选志愿者的概率为
能决定乙当选志愿者的概率为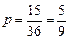 . ……(9分)
. ……(9分)
练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 和棋一局得1分,在甲对乙的每局比赛中,甲胜、负、和的概率依次为0.5,0.3,0.2.现此二人进行两局比赛,得分累加。
和棋一局得1分,在甲对乙的每局比赛中,甲胜、负、和的概率依次为0.5,0.3,0.2.现此二人进行两局比赛,得分累加。 分为
分为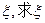 的分布列和期望。
的分布列和期望。


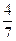
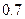 则在这段时间内吊灯能照明的概率是 ( )
则在这段时间内吊灯能照明的概率是 ( )