题目内容
已知函数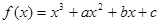 的图象过点
的图象过点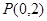 ,且点
,且点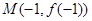 处的切线方程为在
处的切线方程为在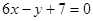 .
.
(1)求函数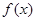 的解析式; (2)求函数
的解析式; (2)求函数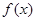 的单调区间。
的单调区间。
(1)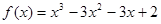
(2)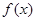 在
在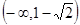 和
和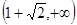 上单调递增,在
上单调递增,在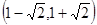 单调递减
单调递减
解析试题分析:因为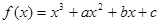 的图象过点
的图象过点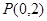 ,且点
,且点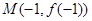 处的切线方程为在
处的切线方程为在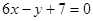 .所以
.所以
(1)由题意得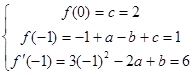 得
得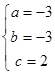 …4分
…4分
故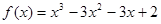 …6分
…6分
(2)
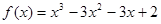 所以
所以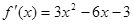
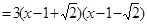
由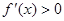 得:
得: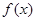 在
在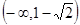 和
和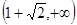 上单调递增;
上单调递增;
由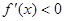 得:
得: 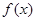 在
在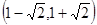 单调递减 …14分
单调递减 …14分
考点:本小题主要考查导数的几何意义的应用和利用导数考查函数的单调性.
点评:导数是研究函数性质尤其是单调性、极值、最值等的有力工具,要牢固掌握,灵活应用.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
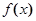 是一次函数,其图像过点
是一次函数,其图像过点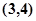 ,且
,且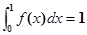 ,求
,求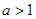 ,函数
,函数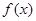 的图像与函数
的图像与函数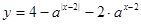 的图像关于点
的图像关于点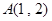 对称.
对称.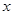 的方程
的方程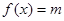 有两个不同的正数解,求实数
有两个不同的正数解,求实数 的取值范围.
的取值范围.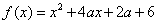 .
. 的值域为
的值域为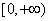 ,求
,求 的值;
的值;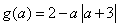 的值域.
的值域.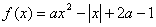 ,(
,( 为实常数)
为实常数)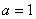 ,将
,将 写出分段函数的形式,并画出简图,指出其单调递减区间;
写出分段函数的形式,并画出简图,指出其单调递减区间;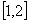 上的最小值为
上的最小值为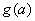 ,求
,求
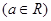 .
.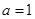 时,证明:
时,证明: 在
在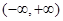 上为减函数;
上为减函数;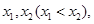 求实数
求实数 的取值范围.
的取值范围.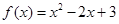 在下列定义域内的值域。
在下列定义域内的值域。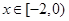 函数y=f(x)的值域
函数y=f(x)的值域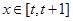 (其中
(其中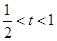 )函数y=f(x)的值域。
)函数y=f(x)的值域。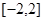 的函数
的函数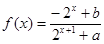 是奇函数.
是奇函数.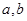 的值; (Ⅱ)解关于
的值; (Ⅱ)解关于 的不等式
的不等式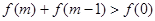 .
.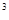 +3x
+3x +9x+a
+9x+a