Question

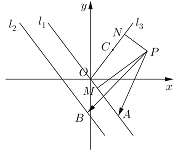
【题目】如图，已知直线和直线，射线的一个法向量为，点为坐标原点，，，点、分别是直线、上的动点，直线和之间的距离为2，于点，于点；

（1）若，求的值；

（2）若，求的最大值；

（3）若，，求的最小值.

Answer 1

【答案】（1）；（2）；（3）.

【解析】

（1）先由得到射线的方程为：，根据点到直线距离公式求出，，由勾股定理求出，，进而可求出结果；

（2）根据题意，得到，设、，得到，，由，结合柯西不等式得到，进而可求出结果；

（3）先由题意，作出点关于直线的对称点，得到，设，

得到，进而可求出结果.

（1）因为，所以，所以射线的方程为：；

所以，，所以；

又直线，所以，所以，

因此；

（2）因为，直线和之间的距离为2，所以，即；

设、，因为，

则，，

所以，

又，所以，

因为，

所以，

故的最大值为；

（3）因为，所以，，如图所示：

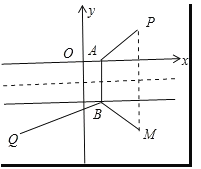
作出点关于直线的对称点，则，

设，

所以，

同理，可由对称性得：当且仅当为时，取得最小值，

因此的最小值为.