题目内容
下列函数 中,①
中,①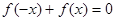 ;②当
;②当 时,都有
时,都有 。同时满足上述两个性质的函数是( )
。同时满足上述两个性质的函数是( )
 中,①
中,①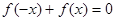 ;②当
;②当 时,都有
时,都有 。同时满足上述两个性质的函数是( )
。同时满足上述两个性质的函数是( )A.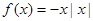 | B. |
C. | D. |
A
解:由①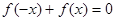 可知,函数y=f(x)为奇函数,②当
可知,函数y=f(x)为奇函数,②当 时,都有
时,都有 中函数单调递减,选项A中,
中函数单调递减,选项A中,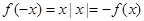 是奇函数,且单调递减;选项B中,
是奇函数,且单调递减;选项B中, ,单调递增,选项C中,
,单调递增,选项C中, 是偶函数,选项D中,
是偶函数,选项D中, ,定义域x>0,不具有奇偶性。因此选A
,定义域x>0,不具有奇偶性。因此选A
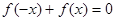 可知,函数y=f(x)为奇函数,②当
可知,函数y=f(x)为奇函数,②当 时,都有
时,都有 中函数单调递减,选项A中,
中函数单调递减,选项A中,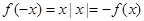 是奇函数,且单调递减;选项B中,
是奇函数,且单调递减;选项B中, ,单调递增,选项C中,
,单调递增,选项C中, 是偶函数,选项D中,
是偶函数,选项D中, ,定义域x>0,不具有奇偶性。因此选A
,定义域x>0,不具有奇偶性。因此选A
练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
 元(
元( )的管理费,预计当每件产品的售价为
)的管理费,预计当每件产品的售价为 元(
元( )时,一年的销售量为
)时,一年的销售量为 万件.
万件.
 ,则一个符合条件的函数表达式为______
,则一个符合条件的函数表达式为______ 与时间
与时间 的关系,可近似地表示为
的关系,可近似地表示为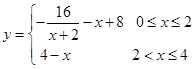 。只有当河流中碱的浓度不低于1时,才能对污染产生有效的抑制作用。
。只有当河流中碱的浓度不低于1时,才能对污染产生有效的抑制作用。 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时, ,则
,则 .
. ,函数
,函数 满足
满足 ”是( )
”是( ) ,
, ,猜想f(x)的表达式为( )
,猜想f(x)的表达式为( )

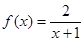

 ,定义
,定义 ,其中,
,其中, ,则
,则 ( )
( )
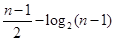


 , 则
, 则 ( )
( )