��Ŀ����
����Ŀ��Ϊ���о�ijѧ�Ƴɼ��Ƿ���ѧ���Ա��йأ����÷ֲ�����ķ������Ӹ߶��꼶��ȡ��![]() ��������
��������![]() ��Ů���ĸ�ѧ�Ƴɼ����õ���ͼ��ʾ�����ɼ���Ƶ�ʷֲ�ֱ��ͼ��Ů���ɼ��ľ�Ҷͼ���涨
��Ů���ĸ�ѧ�Ƴɼ����õ���ͼ��ʾ�����ɼ���Ƶ�ʷֲ�ֱ��ͼ��Ů���ɼ��ľ�Ҷͼ���涨![]() ������Ϊ�ŷ֣���
������Ϊ�ŷ֣���![]() �֣���
�֣���

(1)��i�������ͼʾ����2��2����������������
�ŷ� | ���ŷ� | �ܼ� | |
���� | |||
�� | |||
�ܼ� | 50 |
��ii�����������жϣ��ܷ��ڷ�������ʲ�����![]() ��ǰ������Ϊ��ѧ�Ƴɼ����Ա��й�����
��ǰ������Ϊ��ѧ�Ƴɼ����Ա��й�����
(2)��Ƶ���������ʣ��Ӹ߶��꼶��ѧ�Ƴɼ��������ȡ![]() ��ѧ���ijɼ�����ɼ�Ϊ�ŷ�����
��ѧ���ijɼ�����ɼ�Ϊ�ŷ�����![]() �ķֲ�������ѧ������
�ķֲ�������ѧ������
�ο���ʽ�� ��
��
�ο����ݣ�
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���𰸡���1����i������������������ii�����ڷ�������ʲ�����![]() ��ǰ������Ϊ��ѧ�Ƴɼ����Ա��йأ���2���ֲ��м�������
��ǰ������Ϊ��ѧ�Ƴɼ����Ա��йأ���2���ֲ��м�������![]()
��������
(1)��i�������ͨ������ó�������Ů�����ŷ�����ŷֵ�������Ȼ��������ɣ�
��ii������ͨ��![]() �����������
�����������![]() �Ĺ۲�ֵ��Ȼ����������ݶԱȼ��ɵó������
�Ĺ۲�ֵ��Ȼ����������ݶԱȼ��ɵó������
(2)��ͨ������ó��ŷ�����X���Ӷ���ֲ�![]() ������
������![]() ���ɻ���ɼ�Ϊ�ŷ�����
���ɻ���ɼ�Ϊ�ŷ�����![]() �ķֲ��У�Ȼ����ݶ���ֲ�
�ķֲ��У�Ȼ����ݶ���ֲ�![]() �������
�������![]() .
.
(1)��i������ͼʾ����![]() �����������������£�
�����������������£�
�ŷ� | ���ŷ� | �ܼ� | |
���� | 9 | 21 | 30 |
�� | 11 | 9 | 20 |
�ܼ� | 20 | 30 | 50 |
��ii��![]() �Ĺ۲�ֵ��
�Ĺ۲�ֵ��
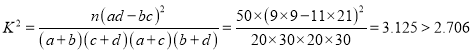 ��
��
�������ڷ�������ʲ�����10%��ǰ������Ϊ��ѧ�Ƴɼ����Ա��йأ�
(2)�����нϴ�İ�����Ϊ��ѧ�Ƴɼ����Ա��йأ�
��˿ɽ���Ů���ɼ����ŷ�Ƶ��![]() �������ʣ�
�������ʣ�
�Ӹ߶��꼶�������ȡ3��ѧ���ĸ�ѧ�Ƴɼ��У�
�ŷ�����![]() ���Ӷ���ֲ�
���Ӷ���ֲ�![]() ��
��
![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
X | 0 | 1 | 2 | 3 |
p |
|
|
|
|
��ѧ����![]() .
.

 Ӣ�żƻ���ĩ����ϵ�д�
Ӣ�żƻ���ĩ����ϵ�д�