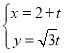题目内容
【题目】设函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)若![]() 在定义域上是增函数,求
在定义域上是增函数,求![]() 的取值范围;
的取值范围;
(2)若直线![]() 是函数
是函数![]() 的切线,求实数
的切线,求实数![]() 的值;
的值;
(3)当![]() 时,证明:
时,证明:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析
;(3)证明见解析
【解析】
(1)首先求出函数的定义域与导函数,由![]() 在
在![]() 上是增函数
上是增函数
即![]() 在
在![]() 上恒成立;即
上恒成立;即![]() 在
在![]() 上恒成立
上恒成立
设![]() ,利用导数说明其单调性,即可求出参数的取值范围;
,利用导数说明其单调性,即可求出参数的取值范围;
(2)设切点为![]() ,则
,则![]() ,再由切线的斜率为零得到
,再由切线的斜率为零得到![]() ,所以
,所以![]() ,构造函数
,构造函数![]() ,利用导数说明其单调性,即可求出参数的值;
,利用导数说明其单调性,即可求出参数的值;
(3)由![]() ,设
,设![]() ,利用导数说明
,利用导数说明![]() 的单调性,即可得到
的单调性,即可得到![]() ,最后利用基本不等式即可得证;
,最后利用基本不等式即可得证;
解:(1)函数![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
∵![]() 在
在![]() 上是增函数
上是增函数
∴![]() 在
在![]() 上恒成立;即
上恒成立;即![]() 在
在![]() 上恒成立
上恒成立
设![]() ,则
,则![]()
由![]() 得
得![]()
∴![]() 在
在![]() 上为增函数;即
上为增函数;即![]()
∴![]() .
.
(2)设切点为![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() ,得
,得![]() ,
,
所以![]() .
.
设![]() ,则
,则![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
所以![]() .
.
因为方程![]() 仅有一解
仅有一解![]() ,
,
所以![]() .
.
(3)因为![]() ,
,
设![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 单调递增.
单调递增.
因为![]() ,
,![]() ,
,
所以存在![]() ,使得
,使得![]() .
.
当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递增,
单调递增,
所以![]() .
.
因为![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]()
![]() .
.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有95%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,再随机抽取3人赠送礼品,记这3人中“微信控”的人数为![]() ,试求
,试求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
【题目】随着手机的发展,“微信”逐渐成为人们支付购物的一种形式.某机构对“使用微信支付”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信支付”赞成人数如下表.
年龄(单位:岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面![]() 列联表,并判断是否有99%
列联表,并判断是否有99%
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若从年龄在![]() 的被调查人中按照赞成与不赞成分层抽样,抽样人数分别3人与2人,现对抽样的5人进行追踪调查,在5人中抽取3人做专访,求3人中不赞成使用微信支付的人数的分布列和期望值.
的被调查人中按照赞成与不赞成分层抽样,抽样人数分别3人与2人,现对抽样的5人进行追踪调查,在5人中抽取3人做专访,求3人中不赞成使用微信支付的人数的分布列和期望值.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
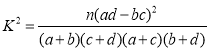 ,其中
,其中![]() .
.
【题目】为了研究某学科成绩是否与学生性别有关,采用分层抽样的方法,从高二年级抽取了![]() 名男生和
名男生和![]() 名女生的该学科成绩,得到如图所示男生成绩的频率分布直方图和女生成绩的茎叶图,规定
名女生的该学科成绩,得到如图所示男生成绩的频率分布直方图和女生成绩的茎叶图,规定![]() 分以上为优分(含
分以上为优分(含![]() 分).
分).

(1)(i)请根据图示,将2×2列联表补充完整;
优分 | 非优分 | 总计 | |
男生 | |||
女生 | |||
总计 | 50 |
(ii)据列联表判断,能否在犯错误概率不超过![]() 的前提下认为“学科成绩与性别有关”?
的前提下认为“学科成绩与性别有关”?
(2)将频率视作概率,从高二年级该学科成绩中任意抽取![]() 名学生的成绩,求成绩为优分人数
名学生的成绩,求成绩为优分人数![]() 的分布列与数学期望.
的分布列与数学期望.
参考公式: .
.
参考数据:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】在2019年高考数学的全国Ⅲ卷中,文科和理科的选做题题目完全相同,第22题考查选修4-4:极坐标和参数方程;第23题考查选修4-5:不等式选讲.某校高三质量检测的命题采用了全国Ⅲ卷的形式,在测试结束后,该校数学组教师对该校全体高三学生的选做题得分情况进行了统计,得到两题得分的![]() 列联表如下(已知每名学生只做了一道题):
列联表如下(已知每名学生只做了一道题):
选做22题 | 选做23题 | 合计 | |
文科人数 | 50 | 60 | |
理科人数 | 40 | ||
总计 | 400 |
(1)完善![]() 列联表中的数据,判断能否有
列联表中的数据,判断能否有![]() 的把握认为“选做题的选择”与“文、理科的科类”有关;
的把握认为“选做题的选择”与“文、理科的科类”有关;
(2)经统计,第23题得分为0的学生中,理科生占理科总人数的![]() ,文科生占文科总人数的
,文科生占文科总人数的![]() ,在按分层抽样的方法在第23题得分为0的学生中随机抽取6名进行单独辅导,并在辅导后随机抽取2名学生进行测试,求被抽中进行测试的2名学生均为理科生的概率.
,在按分层抽样的方法在第23题得分为0的学生中随机抽取6名进行单独辅导,并在辅导后随机抽取2名学生进行测试,求被抽中进行测试的2名学生均为理科生的概率.
附: ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |