题目内容
【题目】新高考方案的考试科目简称“![]() ”,“3”是指统考科目语数外,“1”指在首选科目“物理、历史”中任选1门,“2”指在再选科目“化学、生物、政治和地理”中任选2门组成每位同学的6门高考科目.假设学生在选科中,选修每门首选科目的机会均等,选择每门再选科目的机会相等.
”,“3”是指统考科目语数外,“1”指在首选科目“物理、历史”中任选1门,“2”指在再选科目“化学、生物、政治和地理”中任选2门组成每位同学的6门高考科目.假设学生在选科中,选修每门首选科目的机会均等,选择每门再选科目的机会相等.
(Ⅰ)求某同学选修“物理、化学和生物”的概率;
(Ⅱ)若选科完毕后的某次“会考”中,甲同学通过首选科目的概率是![]() ,通过每门再选科目的概率都是
,通过每门再选科目的概率都是![]() ,且各门课程通过与否相互独立.用
,且各门课程通过与否相互独立.用![]() 表示该同学所选的3门课程在这次“会考”中通过的门数,求随机变量
表示该同学所选的3门课程在这次“会考”中通过的门数,求随机变量![]() 的概率分布和数学期望.
的概率分布和数学期望.
【答案】(Ⅰ)![]() ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
【解析】
(Ⅰ)显然各类别中,一共有![]() 种组合,而选修物理、化学和生物只有一种可能,于是通过古典概率公式即可得到答案;
种组合,而选修物理、化学和生物只有一种可能,于是通过古典概率公式即可得到答案;
(Ⅱ)找出![]() 的所有可能取值有0,1,2,3,依次求得概率,从而得到分布列和数学期望.
的所有可能取值有0,1,2,3,依次求得概率,从而得到分布列和数学期望.
解:(Ⅰ)记“某同学选修物理、化学和生物”为事件![]() ,
,
因为各类别中,学生选修每门课程的机会均等
则![]() ,
,
答:该同学选修物理、化学和生物的概率为![]() .
.
(Ⅱ)随机变量![]() 的所有可能取值有0,1,2,3.
的所有可能取值有0,1,2,3.
因为 ,
,
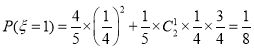 ,
,
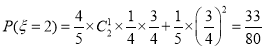 ,
,
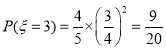 ,
,
所以![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
所以数学期望![]() .
.

练习册系列答案
相关题目
【题目】总体由编号为01,02,03,![]() ,49,50的50个个体组成,利用随机数表(以下选取了随机数表中的第1行和第2行)选取5个个体,选取方法是从随机数表第1行的第9列和第10列数字开始由左向右读取,则选出来的第4个个体的编号为( )
,49,50的50个个体组成,利用随机数表(以下选取了随机数表中的第1行和第2行)选取5个个体,选取方法是从随机数表第1行的第9列和第10列数字开始由左向右读取,则选出来的第4个个体的编号为( )
78 16 65 72 08 02 63 14 07 02 43 69 69 38 74 |
32 04 94 23 49 55 80 20 36 35 48 69 97 28 01 |
A. 05 B. 09 C. 07 D. 20



