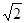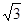题目内容
已知平面α,β,γ,且平面α∥平面β,平面α⊥平面γ;
求证:平面β⊥平面γ
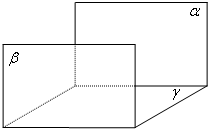
求证:平面β⊥平面γ

证明:如图,
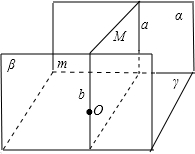
∵平面α⊥平面γ,∴平面α与平面γ相交,设交线为m,
在平面α内作直线a⊥m,∵平面α⊥平面γ,∴a⊥γ,
在平面β内任取一点O,由直线a和点O确定平面M,设M∩β于b,
∵平面α∥平面β,由面面平行的判定定理,得a∥b,
∵a∥b,a⊥γ,∴b⊥γ
又∵b?β,
∴平面β⊥平面γ.

∵平面α⊥平面γ,∴平面α与平面γ相交,设交线为m,
在平面α内作直线a⊥m,∵平面α⊥平面γ,∴a⊥γ,
在平面β内任取一点O,由直线a和点O确定平面M,设M∩β于b,
∵平面α∥平面β,由面面平行的判定定理,得a∥b,
∵a∥b,a⊥γ,∴b⊥γ
又∵b?β,
∴平面β⊥平面γ.

练习册系列答案
相关题目
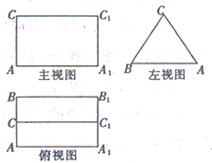
 中,
中,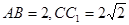 ,
,  为
为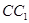 的中点,则点
的中点,则点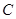 到平面
到平面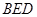 的距离为()
的距离为()