题目内容
4.已知抛物线的图象关于x轴对称,它的顶点是坐标原点,焦点为F,并且经过点M(2,-2).(1)求该抛物线方程及|MF|
(2)若直线y=x-2与抛物线相交于A、B两点,求证:OA⊥OB.
分析 (1)设抛物线方程为y2=mx,代入M(2,-2),求出m,即可求该抛物线方程及|MF|;
(2)先联立直线与抛物线方程消去x,利用韦达定理取得y1+y2和y1y2的值,进而根据直线方程求得x1x2的值,利用x1x2+y1y2=0,即可证明结论.
解答 (1)解:设抛物线方程为y2=mx,
代入M(2,-2),可得4=2m,即有m=2,
则抛物线的方程为y2=2x,|MF|=2+$\frac{1}{2}$=$\frac{5}{2}$.
(2)证明:联立直线与抛物线方程得y2-2y-4=0
∴y1+y2=2,y1y2=-4
∴x1x2=(y1+2)(y2+2)=y1y2+2(y1+y2)+4=4
∴x1x2+y1y2=0
∴$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,
∴$\overrightarrow{OA}$⊥$\overrightarrow{OB}$,
∴OA⊥OB.
点评 本题主要考查抛物线方程,考查直线与抛物线的位置关系.解决的常用方法即为联立方程,消元后利用韦达定理找到解决问题的突破口.

练习册系列答案
相关题目
14.已知M(1,1)、N(3,3)则|MN|=( )
| A. | 8 | B. | 4 | C. | $2\sqrt{2}$ | D. | 2 |
15.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2.若双曲线C上存在一点P,使得△PF1F2为等腰三角形,且cos∠PF1F2=$\frac{1}{8}$,则双曲线的离心率为( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
9.复数z=1+2i的实部与虚部分别为( )
| A. | 1,2 | B. | 1,2i | C. | 2,1 | D. | 2i,1 |
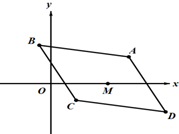 如图,平行四边形ABCD(A,B,C,D按逆时针顺序排列),AB,AD边所在直线的方程分别是x+4y-7=0,3x+2y-11=0,且对角线AC和BD的交点为M(2,0)
如图,平行四边形ABCD(A,B,C,D按逆时针顺序排列),AB,AD边所在直线的方程分别是x+4y-7=0,3x+2y-11=0,且对角线AC和BD的交点为M(2,0)