题目内容
【题目】黑板上写有1,2,…,2014这2014个正整数.现进行如下操作:第一步划去最前面的两个数l、2,并在2014后面写上这两数的和3;第二步划去最前面的三个数3、4、5,并在最后面写上这三数的和12;如此继续下去.当第£步时,黑板上的数不够![]() 个,停止操作.求在黑板上出现过的不同数的个数及这些不同数的和(若一个数多次出现,只计算一次).
个,停止操作.求在黑板上出现过的不同数的个数及这些不同数的和(若一个数多次出现,只计算一次).
【答案】![]()
【解析】
由于第![]() 步后黑板上的数减少
步后黑板上的数减少![]() 个,故
个,故![]()
![]()
![]() .
.
显然,黑板上的所有数之和![]() 是一个不变量.
是一个不变量.
第![]() 步划去的
步划去的![]() 个数为
个数为![]() ,
,
写上的数为![]() .
.
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
故前14步所写的数均小于2014,以后所写的数均大于2014.
第62步划去的数为![]() 这62个数及
这62个数及![]() ,
,
写上的数为![]() .
.
上述所写的新数两两不同,故黑板上出现的不同数有![]() (个).
(个).
黑板上初始的数为![]() ,最后剩下的数之和为
,最后剩下的数之和为![]() ,其中,
,其中,![]() 已出现过,故黑板上出现过的不同数之和为
已出现过,故黑板上出现过的不同数之和为
![]()
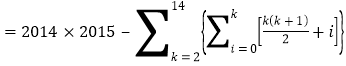
![]() .
.

练习册系列答案
相关题目
【题目】天气预报说,在今后的三天中,每一天下雨的概率均为40%,现部门通过设计模拟实验的方法研究三天中恰有两天下雨的概率:先利用计算器产生0到9之间取整数值的随机数,用1,2,3,4表示下雨,其余6个数字表示不下雨:产生了20组随机数:
907 | 966 | 191 | 925 | 271 | 932 | 812 | 458 | 569 | 683 |
431 | 257 | 393 | 027 | 556 | 488 | 730 | 113 | 537 | 989 |
则这三天中恰有两天降雨的概率约为__________.
【题目】某校有教师400人,对他们进行年龄状况和学历的调查,其结果如下:
学历 | 35岁以下 | 35-55岁 | 55岁及以上 |
本科 |
| 60 | 40 |
硕士 | 80 | 40 |
|
(1)若随机抽取一人,年龄是35岁以下的概率为![]() ,求
,求![]() ;
;
(2)在35-55岁年龄段的教师中,按学历状况用分层抽样的方法,抽取一个样本容量为5的样本,然后在这5名教师中任选2人,求两人中至多有1人的学历为本科的概率.