题目内容
9.已知某几何体的三视图如图所示,则该几何体的体积为( )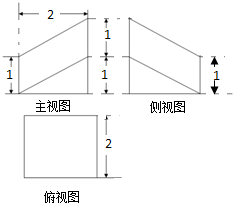
| A. | $\frac{14}{3}$ | B. | 4 | C. | $\frac{10}{3}$ | D. | 3 |
分析 利用三视图作出原几何图形,继而求得体积.
解答 由三视图可得该几何图形为如图所示:
其中,AB=2,AD=GF=1,BC=2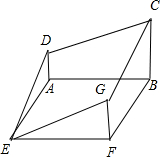

作DH∥AB,连接GH,DG,AF,
则VABEF-CDG=VE-AFGD+VC-DGH+VDGH-ABF,
∴VABEF-CDG=$\frac{1}{3}×1×2\sqrt{2}×\sqrt{2}+\frac{1}{3}×1×\frac{1}{2}×2×2+\frac{1}{2}×2×2×1=4$.
故选:B.
点评 本题主要考查根据三视图作出原几何图形的能力.属基础题型,高考常考题型.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
18.执行下面的程序框图,那么输出的S等于( )
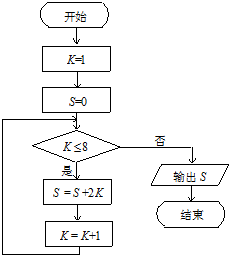

| A. | 42 | B. | 56 | C. | 72 | D. | 90 |
6.已知$\overrightarrow{e}$和$\overrightarrow{f}$是互相垂直的单位向量,向量$\overrightarrow{{a}_{n}}$满足:$\overrightarrow{e}•\overrightarrow{{a}_{n}}$=n,$\overrightarrow{f}•\overrightarrow{{a}_{n}}$=2n,n∈N*,设θn为$\overrightarrow{{a}_{n+1}}$-$\overrightarrow{{a}_{n}}$和$\overrightarrow{{a}_{n+2}}$-$\overrightarrow{{a}_{n+1}}$的夹角,则( )
| A. | θn随着n的增大而增大 | B. | θn随着n的增大而减小 | ||
| C. | 随着n的增大,θn先增大后减小 | D. | 随着n的增大,θn先减小后增大 |

 某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.