题目内容
1.若正实数a、b、c满足a+b+c=3,ab+bc+ac=2,则a+b的最小值是$\frac{6-2\sqrt{3}}{3}$.分析 由已知得到c=3-(a+b),代入ab+bc+ac=2,利用基本不等式转化为关于(a+b)的不等式,求解不等式得a+b的最小值.
解答 解:∵a+b+c=3,∴c=3-(a+b),
由ab+bc+ac=2,得ab+c(a+b)=2.
∴ab=(a+b)2-3(a+b)+2$≤\frac{(a+b)^{2}}{4}$,
∴3(a+b)2-12(a+b)+8≤0,
解得:$a+b≥\frac{6-2\sqrt{3}}{3}$.
故答案为:$\frac{6-2\sqrt{3}}{3}$.
点评 本题考查了基本不等式在最值中的应用,考查了数学转化思想方法,是中档题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
10.在△ABC中,内角A,B,C的对边分别是a,b,c,若a2-b2=$\sqrt{3}$bc,sinC=$\sqrt{3}$sinB,则A=( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
9.已知某几何体的三视图如图所示,则该几何体的体积为( )
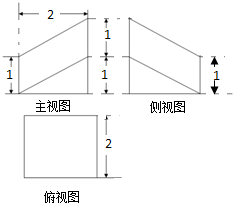

| A. | $\frac{14}{3}$ | B. | 4 | C. | $\frac{10}{3}$ | D. | 3 |
 如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,…,依此类推.现有一颗小弹子从第一层的通道里向下运动.若在通道的分叉处,小弹子以相同的概率落入每个通道,记小弹子落入第n层第m个竖直通道(从左至右)的概率为P(n,m).某研究性学习小组经探究发现小弹子落入第n层的第m个通道的次数服从二项分布,请你解决下列问题.
如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,…,依此类推.现有一颗小弹子从第一层的通道里向下运动.若在通道的分叉处,小弹子以相同的概率落入每个通道,记小弹子落入第n层第m个竖直通道(从左至右)的概率为P(n,m).某研究性学习小组经探究发现小弹子落入第n层的第m个通道的次数服从二项分布,请你解决下列问题. 如图AB是圆O的一条弦,过点A作圆的切线AD,作BD⊥AD,与该圆交于点E,若AD=2$\sqrt{3}$,DE=2.
如图AB是圆O的一条弦,过点A作圆的切线AD,作BD⊥AD,与该圆交于点E,若AD=2$\sqrt{3}$,DE=2.