题目内容
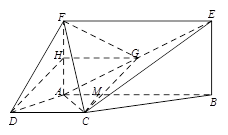
如图,已知四边形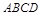 为梯形,
为梯形,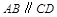 ,
,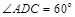 ,四边形
,四边形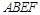 为矩形,且平面
为矩形,且平面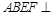 平面
平面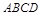 ,
, ,点
,点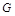 为
为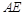 的中点.
的中点.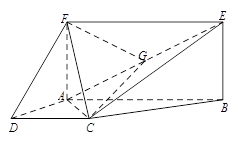
(Ⅰ)求证: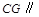 平面
平面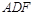 ;
;
(Ⅱ)求证:平面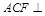 平面
平面 ;
;
(Ⅲ)求三棱锥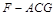 的体积.
的体积.
(Ⅰ)详见解析;(Ⅱ)详见解析;(Ⅲ)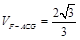 .
.
解析试题分析:(Ⅰ)取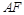 中点
中点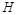 ,可以证明四边形
,可以证明四边形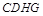 为平行四边形,即
为平行四边形,即 ,∴
,∴ ∥平面
∥平面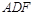 ;
;
(Ⅱ)证明 平面
平面 即可;(Ⅲ)改变四面体(三棱锥)的顶点,取C即可;或者利用比例.
即可;(Ⅲ)改变四面体(三棱锥)的顶点,取C即可;或者利用比例.
试题解析:(Ⅰ)取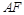 中点
中点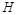 ,连
,连 .
.
∵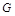 为对角线
为对角线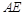 的中点,∴
的中点,∴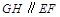 ,且
,且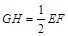 ,
,
∴四边形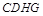 为平行四边形,即
为平行四边形,即 ;或者可以采用比例的方法求解.
;或者可以采用比例的方法求解.
又∵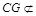 平面
平面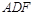 ,
, 平面
平面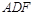 ,∴
,∴ ∥平面
∥平面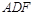 . 4分
. 4分
(Ⅱ)∵四边形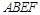 为矩形,且平面
为矩形,且平面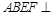 平面
平面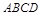 ,∴
,∴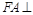 平面
平面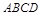 ,∴
,∴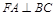 ;
;
∵四边形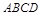 为梯形,
为梯形,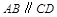 ,且
,且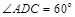 ,∴
,∴ .
.
又在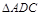 中,
中,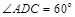 ,且
,且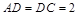 ,∴
,∴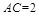 ,
,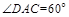 ,∴
,∴ .
.
于是在 中,由
中,由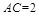 ,
, ,
, 及余弦定理,得
及余弦定理,得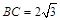 .
.
∴ ,∴
,∴ .∴
.∴ 平面
平面 ,
,
又∵ 平面
平面 ,∴平面
,∴平面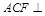 平面
平面 . 9分
. 9分
(Ⅲ)作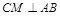 ,垂足为
,垂足为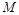 ,由平面
,由平面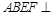 平面
平面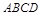 得
得 平面
平面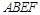 .
.
易求得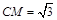 ,所以三棱锥
,所以三棱锥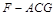 的体积为
的体积为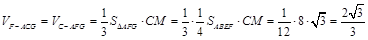 . 13分.
. 13分.
【法二】连接 ,则
,则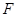 、
、 、
、 三点共线,故
三点共线,故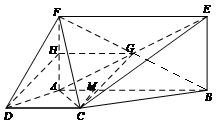

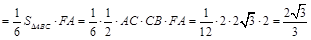
考点:线面位置关系的证明、多面体体积的计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
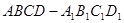 的底面
的底面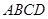 是平行四边形,且
是平行四边形,且 ,
,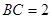 ,
,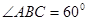 ,
, 为
为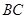 的中点,
的中点,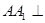 平面
平面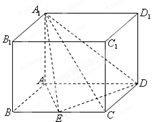
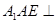 平面
平面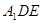 ;
;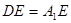 ,试求异面直线
,试求异面直线 与
与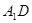 所成角的余弦值;
所成角的余弦值;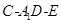 的余弦值.
的余弦值.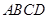 的边长为4,
的边长为4,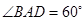 ,
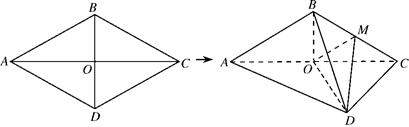
,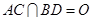 .将菱形
.将菱形 折起,得到三棱锥
折起,得到三棱锥 ,点
,点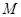 是棱
是棱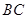 的中点,
的中点, .
.
 平面
平面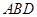 ;
;
 平面
平面 ;
; 的体积.
的体积.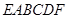 的底面
的底面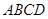 是边长为
是边长为 的正方形,
的正方形,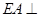 底面
底面 ,且
,且 .
. 平行,要求保留作图痕迹,但不要求证明.
平行,要求保留作图痕迹,但不要求证明.
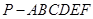 的底面是边长为1的正六边形,
的底面是边长为1的正六边形,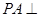 底面
底面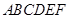 。
。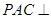 平面
平面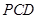 ;
;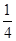 ,求六棱锥
,求六棱锥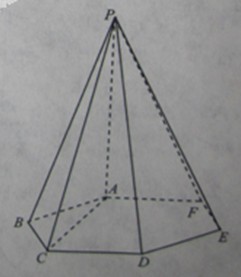
 中,
中,
 为
为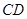 的中点,沿
的中点,沿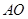 将三角形
将三角形 折起,使
折起,使 .
. ;
;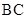 与平面
与平面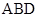 所成角的正弦值.
所成角的正弦值.
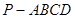 中,
中, 底面
底面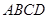 ,面
,面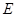 为侧棱
为侧棱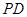 上一点,
上一点, 为
为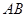 上一点.该四棱锥的正(主)视图和侧(左)视图如图2所示.
上一点.该四棱锥的正(主)视图和侧(左)视图如图2所示.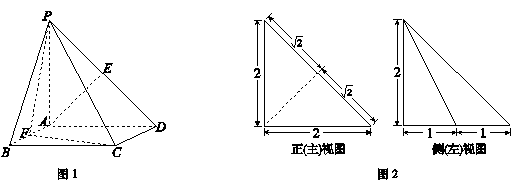
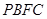 的体积;
的体积;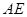 ∥平面
∥平面 ;
;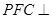 平面
平面 .
. 所在的平面与正方形
所在的平面与正方形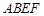 所在的平面相互垂直,
所在的平面相互垂直,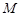 、
、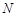 分别是
分别是 、
、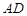 的中点.
的中点.
 面
面 ;
; 与平面
与平面 所成的角正弦值.
所成的角正弦值.