题目内容
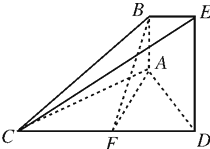
如图,正方形 所在的平面与正方形
所在的平面与正方形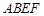 所在的平面相互垂直,
所在的平面相互垂直,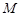 、
、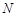 分别是
分别是 、
、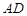 的中点.
的中点.
(1)求证:面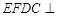 面
面 ;
;
(2)求直线 与平面
与平面 所成的角正弦值.
所成的角正弦值.
(1)详见解析;(2)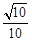 .
.
解析试题分析:(1)采用思路:线线垂直推出线面垂直,然后推出面面垂直;(2)利用定义法通过添加辅助线确定直线 与平面
与平面 所成的角,然后通过解三角形求解其值.
所成的角,然后通过解三角形求解其值.
试题解析:(1)∵ 为正方形,∴
为正方形,∴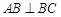
又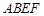 为正方形,∴
为正方形,∴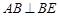 ,∴
,∴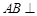 面
面 . 3分
. 3分
又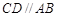 ,∴
,∴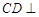 面
面 .
.
而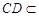 面
面 ,∴面
,∴面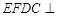 面
面 . 6分
. 6分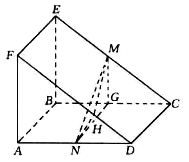
(Ⅱ)作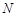 在
在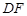 上的射影
上的射影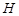 ,连
,连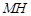 . 7′
. 7′
∵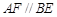 ,
,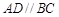 ,∴面
,∴面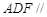 面
面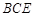 ,
,
∴面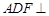 面
面 ,∴
,∴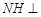 面
面 ,
,
∴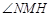 为
为 与面
与面 所成的角. 9分
所成的角. 9分
作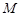 在
在 上的射影
上的射影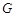 ,连
,连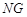 .
.
设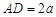 ,则
,则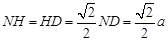 ,
,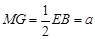 .
.
∴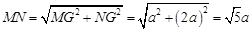
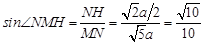 ,
,
∴直线 与平面
与平面 所成的角的正弦值为
所成的角的正弦值为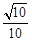 . 12分
. 12分
考点:1.面面垂直的证明;(2)线面角.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
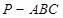 中,
中,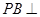 底面
底面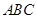 ,
,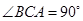 ,
,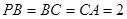 ,
,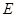 为
为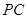 的中点,点
的中点,点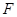 在
在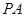 上,且
上,且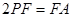 .
.
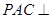 平面
平面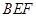 ;
;  与平面
与平面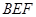 所成的二面角的平面角(锐角)的余弦值.
所成的二面角的平面角(锐角)的余弦值.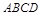 为梯形,
为梯形,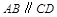 ,
,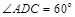 ,四边形
,四边形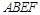 为矩形,且平面
为矩形,且平面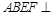 平面
平面 ,点
,点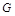 为
为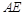 的中点.
的中点.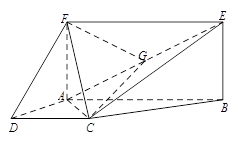
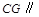 平面
平面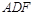 ;
;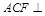 平面
平面 ;
;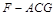 的体积.
的体积.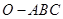 的侧棱
的侧棱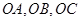 两两垂直,且
两两垂直,且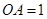 ,
,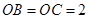 ,
, 是
是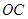 的中点.(1)求
的中点.(1)求 点到面
点到面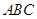 的距离;(2)求二面角
的距离;(2)求二面角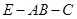 的正弦值.
的正弦值.
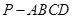 中,
中, 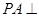 平面
平面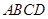 ,
,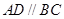 ,
,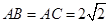 ,
,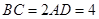 .
. 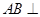 平面
平面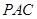 ;
;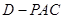 的高.
的高. 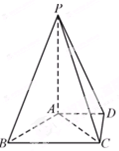
 中,
中,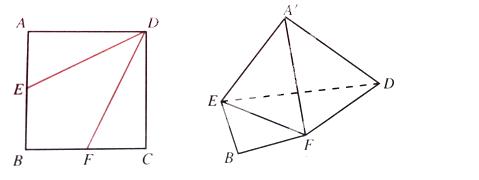
 是
是 的中点,点
的中点,点 是
是 的中点,将
的中点,将 分别沿
分别沿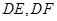 折起,使
折起,使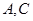 两点重合于点
两点重合于点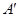 。求证:
。求证:
 时,求三棱锥
时,求三棱锥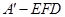 的体积。
的体积。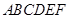 中,四边形
中,四边形 是边长为
是边长为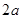 的正方形,平面
的正方形,平面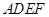 垂直于平面
垂直于平面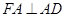 ,
,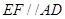 ,
,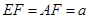 .
.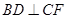 ;
;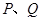 分别为棱
分别为棱 和
和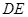 的中点,求证:
的中点,求证: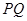 ∥平面
∥平面
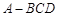 中,
中,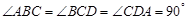 ,
,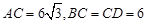 ,设顶点
,设顶点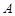 在底面
在底面 上的射影为
上的射影为 .
.
 ;
;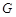 在棱
在棱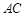 上,且
上,且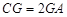 ,试求二面角
,试求二面角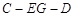 的余弦值.
的余弦值.