题目内容
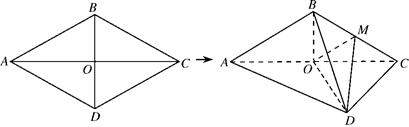
如图,菱形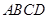 的边长为4,
的边长为4,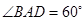 ,
,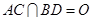 .将菱形
.将菱形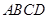 沿对角线
沿对角线 折起,得到三棱锥
折起,得到三棱锥 ,点
,点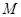 是棱
是棱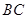 的中点,
的中点, .
.
(1)求证: 平面
平面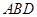 ;
;
(2)求证:平面
 平面
平面 ;
;
(3)求三棱锥 的体积.
的体积.
(1)详见解析;(2)详见解析;(3)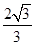 .
.
解析试题分析:(1)利用三角形的中位线平行于相应的底边证明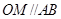 ,然后结合直线与平面平行的判定定理即可证明
,然后结合直线与平面平行的判定定理即可证明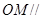 平面
平面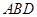 ;(2)先利用翻折时
;(2)先利用翻折时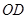 与
与 的相对位置不变证明
的相对位置不变证明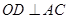 ,然后利用勾股定理证明
,然后利用勾股定理证明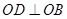 ,并结合直线与平面垂直的判定定理先证明
,并结合直线与平面垂直的判定定理先证明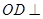 平面
平面 ,最终利用平面与平面垂直的判定定理证明平面
,最终利用平面与平面垂直的判定定理证明平面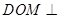 平面
平面 ;(3)利用(2)中的结论
;(3)利用(2)中的结论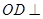 平面
平面 ,利用等体积法将三棱锥
,利用等体积法将三棱锥 的体积转化为以点
的体积转化为以点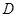 为顶点,
为顶点,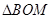 所在平面为底面的三棱锥
所在平面为底面的三棱锥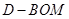 的体积来计算,则三棱锥的高为
的体积来计算,则三棱锥的高为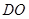 ,
,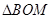 的面积为底面积,然后利用锥体的体积公式即可计算三棱锥
的面积为底面积,然后利用锥体的体积公式即可计算三棱锥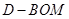 的体积,在计算
的体积,在计算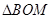 的面积时,首先应确定
的面积时,首先应确定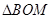 的形状,然后选择合适的公式计算计算
的形状,然后选择合适的公式计算计算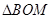 的面积.
的面积.
试题解析:(1)因为O为AC的中点,M为BC的中点,所以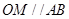 .
.
因为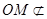 平面ABD,
平面ABD,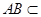 平面ABD,所以
平面ABD,所以 平面
平面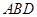 .
.
(2)因为在菱形ABCD中,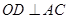 ,所以在三棱锥
,所以在三棱锥 中,
中,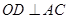 .
.
在菱形ABCD中,AB=AD=4,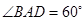 ,所以BD=4.因为O为BD的中点,
,所以BD=4.因为O为BD的中点,
所以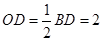 .因为O为AC的中点,M为BC的中点,所以
.因为O为AC的中点,M为BC的中点,所以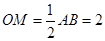 .
.
因为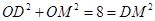 ,所以
,所以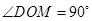 ,即
,即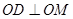 .
.
因为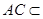 平面ABC,
平面ABC,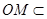 平面ABC,
平面ABC,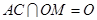 ,所以
,所以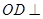 平面ABC.
平面ABC.
因为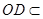 平面DOM,所以平面
平面DOM,所以平面
 平面
平面 .
.
(3)由(2)得,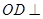 平面BOM,所以
平面BOM,所以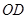 是三棱锥
是三棱锥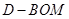 的高.
的高.
因为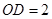 ,
, ,
,
所以 .
.
考点:直线与平面平行、平面与平面平行、等体积法

练习册系列答案
相关题目
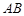 是圆的直径,
是圆的直径,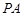 垂直于圆所在的平面,
垂直于圆所在的平面,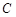 是圆上的点.
是圆上的点.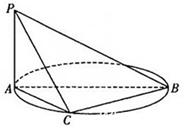
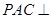 平面
平面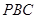 ;
;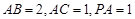 ,求二面角
,求二面角 的余弦值.
的余弦值.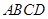 为矩形,平面
为矩形,平面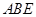 ,
,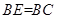 ,
,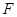 为
为 上的一点,且
上的一点,且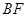 ⊥平面
⊥平面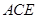 .
. 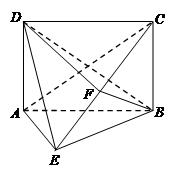
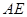 ⊥
⊥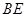 ;
;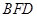 .
.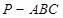 中,
中,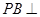 底面
底面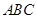 ,
,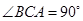 ,
,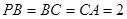 ,
,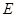 为
为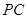 的中点,点
的中点,点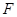 在
在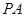 上,且
上,且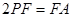 .
.
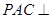 平面
平面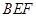 ;
;  与平面
与平面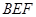 所成的二面角的平面角(锐角)的余弦值.
所成的二面角的平面角(锐角)的余弦值.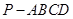 中,侧棱
中,侧棱 底面
底面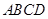 ,底面
,底面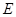 为
为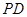 上一点,
上一点,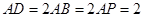 ,
,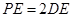 .
.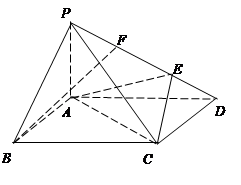
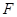 为
为 的中点,求证
的中点,求证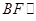 平面
平面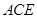 ;
; 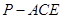 的体积.
的体积. 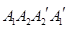 ,满足
,满足 在
在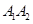 上,
上,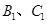 在
在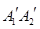 上,且
上,且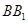 ∥
∥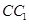 ∥
∥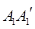 ,
,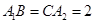 ,
,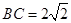 ,
,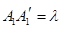 ,沿
,沿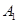 与
与 、
、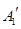 与
与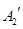 重合后分别记为
重合后分别记为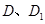 ,在直三棱柱
,在直三棱柱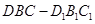 中,点
中,点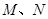 分别为
分别为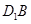 和
和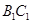 的中点.
的中点.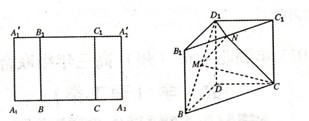
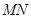 ∥平面
∥平面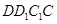 ;
;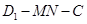 为直二面角,求
为直二面角,求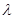 的值.
的值.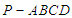 中,底面
中,底面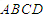 为菱形,
为菱形,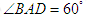 ,
,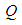 为
为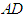 的中点。
的中点。
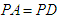 ,求证:平面
,求证:平面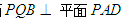 ;
;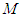 在线段
在线段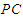 上,
上,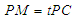 ,试确定
,试确定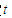 的值,使
的值,使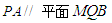 ;
;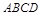 为梯形,
为梯形,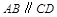 ,
,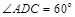 ,四边形
,四边形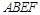 为矩形,且平面
为矩形,且平面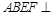 平面
平面 ,点
,点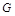 为
为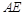 的中点.
的中点.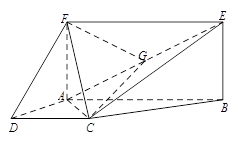
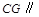 平面
平面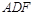 ;
;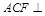 平面
平面 ;
;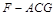 的体积.
的体积.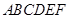 中,四边形
中,四边形 是边长为
是边长为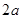 的正方形,平面
的正方形,平面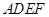 垂直于平面
垂直于平面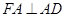 ,
,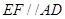 ,
,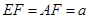 .
.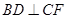 ;
;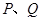 分别为棱
分别为棱 和
和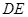 的中点,求证:
的中点,求证: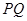 ∥平面
∥平面