题目内容
【题目】已知函数f（x）=lnx+x2 ．
（Ⅰ）若函数g（x）=f（x）﹣ax在其定义域内为增函数，求实数a的取值范围；
（Ⅱ）在（Ⅰ）的条件下，若a＞1，h（x）=e3x﹣3aexx∈[0，ln2]，求h（x）的极小值；
（Ⅲ）设F（x）=2f（x）﹣3x2﹣kx（k∈R），若函数F（x）存在两个零点m，n（0＜m＜n），且2x0=m+n．问：函数F（x）在点（x0 ， F（x0））处的切线能否平行于x轴？若能，求出该切线方程；若不能，请说明理由．
【答案】解：（Ⅰ）g（x）=f（x）﹣ax=lnx+x2﹣ax， 
由题意知，g′（x）≥0，对任意的x∈（0，+∞）恒成立，即 
又∵x＞0， 
，当且仅当 
时等号成立
∴ 
，可得 
（Ⅱ）由（Ⅰ）知， 
，令t=ex，则t∈[1，2]，则
h（t）=t3﹣3at， 
由h′（t）=0，得 
或 
（舍去），
∵ ，∴ 
若 
，则h′（t）＜0，h（t）单调递减；若 
，则h′（t）＞0，h（t）单调递增
∴当 时，h（t）取得极小值，极小值为 
（Ⅲ）设F（x）在（x0，F（x0））的切线平行于x轴，其中F（x）=2lnx﹣x2﹣kx
结合题意，有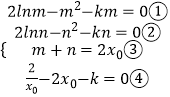 
①﹣②得 
所以 
，由④得 
所以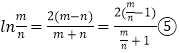 
设 
，⑤式变为 
设 
， 
所以函数 
在（0，1）上单调递增，
因此，y＜y|u=1=0，即 
，也就是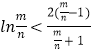 
此式与⑤矛盾
所以F（x）在（x0，F（x0））的切线不能平行于x轴
【解析】（1）根据f（x）的解析式，写出g（x）的解析式，求导，由于g（x）单调递增，可得出
在
恒大于零，进行参变分离求出a的取值范围；（2）令
进行换元，讨论t的范围，求出h（t）的单调区间，找出函数的最小值；（3）先设F（x）在
的切线平行于x轴由题意得出方程组，换元研究单调性，证出在（0,1）上成立，从而与题设矛盾，故函数F（x）在处的切线不平行于x轴。
