题目内容
【题目】在直角坐标系中,圆C1:x2+y2=1经过伸缩变换 ![]() 后得到曲线C2以坐标原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线l的极坐标方程为cosθ+2sinθ=
后得到曲线C2以坐标原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线l的极坐标方程为cosθ+2sinθ= ![]()
(1)求曲线C2的直角坐标方程及直线l的直角坐标方程;
(2)在C2上求一点M,使点M到直线l的距离最小,并求出最小距离.
【答案】
(1)解:∵ ![]() 后得到曲线C2,
后得到曲线C2,
∴ 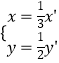 ,代入圆C1:x2+y2=1得:
,代入圆C1:x2+y2=1得: ![]() ,
,
故曲线C2的直角坐标方程为 ![]() ;
;
直线l的极坐标方程为cosθ+2sinθ= ![]() .
.
即ρcosθ+2ρsinθ=10,即x+2y﹣10=0,
(2)将直线x+2y﹣10=0平移与C2相切时,则第一象限内的切点M满足条件,
设过M的直线为x+2y+C=0,
则由 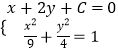 得:
得: ![]() x2+
x2+ ![]() Cx+
Cx+ ![]() C2﹣36=0,
C2﹣36=0,
由△=( ![]() C)2﹣4×
C)2﹣4× ![]() ×(
×( ![]() C2﹣36)=0得:C=±
C2﹣36)=0得:C=± ![]() ,
,
故x= ![]() ,或x=﹣
,或x=﹣ ![]() ,(舍去),
,(舍去),
则y= ![]() ,
,
即M点的坐标为( ![]() ,
, ![]() ),
),
则点M到直线l的距离d= ![]() =
= ![]()
【解析】(1)圆![]() 经过伸缩变换后得到的是椭圆,本题关键在于将
经过伸缩变换后得到的是椭圆,本题关键在于将![]() 变为
变为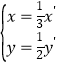 带入圆
带入圆![]() 的方程从而得出结果,极坐标方程化为直角坐标方程需要用到极化直公式
的方程从而得出结果,极坐标方程化为直角坐标方程需要用到极化直公式
(2)必需要求出点M的坐标,而满足条件的点M 是直线x+2y+C=0与椭圆的切点,从而联立方程组求出点M的坐标

练习册系列答案
相关题目