[题目]已知函数f(A＞0.ω＞0.﹣ ＜φ＜0)的图象与y轴的交点为(0.1).它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0 . 2)和(x0+2π.﹣2)．的解析式,(2)若锐角θ满足f(2θ+ )= .求f(2θ)的值．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知函数f（x）=Acos（ωx+φ）（A＞0，ω＞0，﹣ ＜φ＜0）的图象与y轴的交点为（0，1），它在y轴右侧的第一个最高点和第一个最低点的坐标分别为（x0 ， 2）和（x0+2π，﹣2）．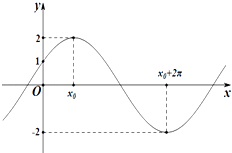

（1）求函数f（x）的解析式；
（2）若锐角θ满足f（2θ+ ）= ，求f（2θ）的值．

【答案】
（1）解：由题意可得A=2， = =2π，解得ω= ，

∴f（x）=2cos（ x+φ），

由图象可知f（0）=2cosφ=1，∴cosφ= ，

又﹣ ＜φ＜0，∴φ=﹣

∴f（x）=2cos（ x﹣ ）

（2）∵ ，∴2cosθ= ，

∴cosθ= ，∵θ为锐角，∵sinθ=

∴f（2θ）=2cos（θ﹣ ）=2（ cosθ+ sinθ）

=2（ + ）= ，

即f（2θ）的值为

【解析】（1）根据图象可得A=2，周期为4，由周期公式解得，图像过点,代入解析式，可求得；（2）由,解得的正余弦值，再通过三角恒等变换计算

练习册系列答案

相关题目

【题目】已知数列{an}与{bn}满足an+1﹣an=2（bn+1﹣bn），n∈N+ ， bn=2n﹣1，且a1=2．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设，Tn为数列{cn}的前n项和，求Tn ．

【题目】已知函数，．
（1）求函数f（x）的值域；
（2）已知锐角△ABC的两边长a，b分别为函数f（x）的最小值与最大值，且△ABC的外接圆半径为，求△ABC的面积．

【题目】记等差数列{an}的前n项和为Sn ．
（1）求证：数列{ }是等差数列；
（2）若a1=1，对任意的n∈N*，n≥2，均有，，是公差为1的等差数列，求使为整数的正整数k的取值集合；
（3）记bn=a （a＞0），求证： ≤ ．

【题目】设数列{an}是各项均为正数的等比数列，其前n项和为Sn ，且a1a5=64，S5﹣S3=48．
（1）求数列{an}的通项公式；
（2）设有正整数m，l（5＜m＜l），使得am ， 5a5 ， al成等差数列，求m，l的值；
（3）设k，m，l∈N*，k＜m＜1，对于给定的k，求三个数 5ak ， am ， al经适当排序后能构成等差数列的充要条件．

【题目】已知函数f（x）=lnx+x2 ．
（Ⅰ）若函数g（x）=f（x）﹣ax在其定义域内为增函数，求实数a的取值范围；
（Ⅱ）在（Ⅰ）的条件下，若a＞1，h（x）=e3x﹣3aexx∈[0，ln2]，求h（x）的极小值；
（Ⅲ）设F（x）=2f（x）﹣3x2﹣kx（k∈R），若函数F（x）存在两个零点m，n（0＜m＜n），且2x0=m+n．问：函数F（x）在点（x0 ， F（x0））处的切线能否平行于x轴？若能，求出该切线方程；若不能，请说明理由．

【题目】如图，在△ABC中，角A，B，C所对的边分别为a，b，c，且3bsinA=c，D为AC边上一点．

（1）若D是AC的中点，且，，求△ABC的最短边的边长．
（2）若c=2b=4，S△BCD= ，求DC的长．

【题目】直线x+2y=m（m＞0）与⊙O：x2+y2=5交于A，B两点，若| + |＞2| |，则m的取值范围是（　　）
A.
B.
C.
D.

【题目】某公司对应聘人员进行能力测试，测试成绩总分为150分．下面是30位应聘人员的测试成绩的测试成绩：64，116，82，93，102，82，104，67，93，118，70，95，119，106，83，72，95，106，72，119，122，95，86，74，131，76，88，108，97，123．
（1）求应聘人员的测试成绩的样本平均数（保留小数点后两位）；
（2）根据以上数据完成下面茎叶图：

应聘人员的测试成绩
6
7
8
9
10
11
12
13

（3）由茎叶图可以认为，应聘人员的测试成绩Z服从正态分布N（μ，σ2），其中μ近似为样本平均数，σ2近似为样本方差s2 ，其中s2=18.872 ，利用该正态分布，求P（76.40＜Z＜114.14）．
附：若Z～N（μ，σ2），则P（μ﹣σ＜Z＜μ+σ）=0.6826，
P（μ﹣2σ＜Z＜μ+2σ）=0.9544．

试题分类