题目内容
已知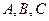 是长轴为4的椭圆上的三点,点
是长轴为4的椭圆上的三点,点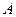 是长轴的一个顶点,
是长轴的一个顶点,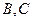 过椭圆中心
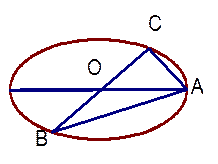
过椭圆中心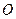 (如图),且
(如图),且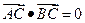 ,
,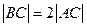
(I)求椭圆的方程;
 (Ⅱ)如果椭圆上的两点
(Ⅱ)如果椭圆上的两点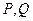 ,使
,使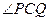 的平分线垂直于
的平分线垂直于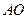 ,是否总存在实数
,是否总存在实数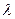 ,使
,使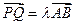 。请给出证明。
。请给出证明。
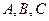 是长轴为4的椭圆上的三点,点
是长轴为4的椭圆上的三点,点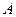 是长轴的一个顶点,
是长轴的一个顶点,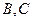 过椭圆中心
过椭圆中心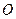 (如图),且
(如图),且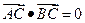 ,
,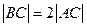
(I)求椭圆的方程;
 (Ⅱ)如果椭圆上的两点
(Ⅱ)如果椭圆上的两点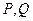 ,使
,使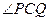 的平分线垂直于
的平分线垂直于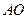 ,是否总存在实数
,是否总存在实数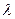 ,使
,使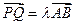 。请给出证明。
。请给出证明。)
由条件,设所求的椭圆方程为 其 中
其 中 

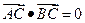 ,
,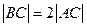 则
则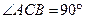 ,且
,且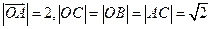
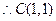 代入椭圆方程得
代入椭圆方程得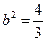
即椭圆方程为
(Ⅱ)若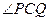 的平分线垂直于
的平分线垂直于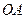 ,则
,则 倾斜角互补,设
倾斜角互补,设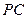 所在的直线方程为
所在的直线方程为 由方程组
由方程组
 可得
可得 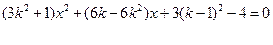
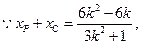 且
且 ,代入
,代入 中可得
中可得
同理可得
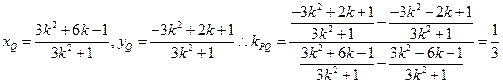
又 总存在
总存在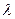 使
使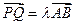
由条件,设所求的椭圆方程为
 其 中
其 中 

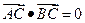 ,
,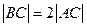 则
则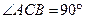 ,且
,且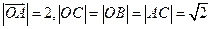
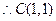 代入椭圆方程得
代入椭圆方程得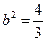
即椭圆方程为

(Ⅱ)若
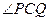 的平分线垂直于
的平分线垂直于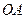 ,则
,则 倾斜角互补,设
倾斜角互补,设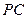 所在的直线方程为
所在的直线方程为 由方程组
由方程组 可得
可得 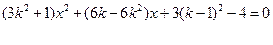
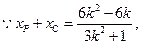 且
且 ,代入
,代入 中可得
中可得
同理可得
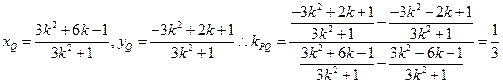
又
 总存在
总存在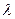 使
使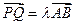
略

练习册系列答案
相关题目
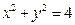 外一点
外一点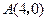 ,作圆的割线,求割线被圆截得的弦的中点的轨迹方程.
,作圆的割线,求割线被圆截得的弦的中点的轨迹方程.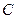 的顶点在原点,焦点在
的顶点在原点,焦点在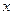 轴上,斜率为
轴上,斜率为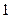 的直线交
的直线交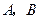 两点,若
两点,若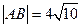 ,且以
,且以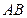 为直径的圆经过原点
为直径的圆经过原点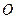 ,求直线
,求直线 和抛物线
和抛物线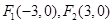 ,一条渐近线方程为
,一条渐近线方程为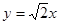 ,则该双曲线的方程为________________
,则该双曲线的方程为________________
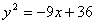 的顶点和准线.
的顶点和准线. 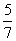 ,求点P到x轴的距离;
,求点P到x轴的距离;
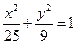 上一点
上一点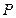 ,它到左准线的距离为
,它到左准线的距离为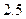 ,求点
,求点