题目内容
【题目】已知定义域为![]() 的函数
的函数![]() 是奇函数.
是奇函数.
(1)求![]() 的值;
的值;
(2)判断函数![]() 的单调性,并用定义证明;
的单调性,并用定义证明;
(3)当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2) 减函数,证明见解析;(3)
(2) 减函数,证明见解析;(3) ![]() .
.
【解析】
(1)利用奇函数的性质令![]() ,求解
,求解![]() 即可.
即可.
(2)利用函数的单调性的定义证明即可.
(3)利用函数是奇函数以及函数的单调性转化不等式为代数形式的不等式,求解即可.
(1)∵![]() 在定义域
在定义域![]() 上是奇函数,
上是奇函数,
所以![]() ,即
,即![]() ,∴
,∴![]() ,
,
经检验,当![]() 时,原函数是奇函数.
时,原函数是奇函数.
(2)![]() 在
在![]() 上是减函数,证明如下:
上是减函数,证明如下:
由(1)知![]() ,
,
任取![]() ,设
,设![]() ,
,
则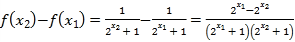 ,
,
∵函数![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() ,即
,即![]() ,
,
∴函数![]() 在
在![]() 上是减函数.
上是减函数.
(3)因![]() 是奇函数,从而不等式
是奇函数,从而不等式![]() 等价于
等价于![]() ,
,
由(2)知![]() 在
在![]() 上是减函数,由上式推得
上是减函数,由上式推得![]() ,
,
即对任意![]() ,有
,有![]() 恒成立,
恒成立,
由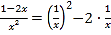 ,
,
令![]() ,
,![]() ,则可设
,则可设![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目