题目内容
【题目】已知命题P：不等式
的解集中的整数有且仅有-1，0，1.求a的取值范围.
命题Q：集合
且
.
（1）分别求命题P、Q为真命题时的实数a的取值范围；
（2）当实数a取何值时，命题P、Q中有且仅有一个为真命题；
（3）设P、Q皆为真时a的取值范围为集合S，
，若全集
，
，求实数m的取值范围.
【答案】（1）
，
；（2）
；（3）
.
【解析】
（1）解不等式得到
，根据整数解得到不等式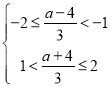
解得答案；讨论
和
两种情况，分别计算得到答案.
（2）讨论当
真
假时和当真假时两种情况，分别计算得到答案.
（3）根据
得到
，计算
，得到
，根据范围大小得到答案.
（1）
则，解集中的整数有且仅有-1，0，1.
则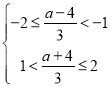 解得：
且
当时：
解得
；
当时：
且
解得
综上所述：
（2）当真假时：不成立；当真假时：
综上所述：
（3）
，
利用均值不等式
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
