题目内容
【题目】已知函数 ![]()
(1)求函数 ![]() 的定义域;
的定义域;
(2)若存在a∈R,对任意 ![]() ,总存在唯一x0∈[﹣1,2],使得f(x1)=g(x0)成立.求实数a的取值范围.
,总存在唯一x0∈[﹣1,2],使得f(x1)=g(x0)成立.求实数a的取值范围.
【答案】
(1)解:由 ![]() ,解得
,解得 ![]() ,k∈Z,解得2kπ﹣
,k∈Z,解得2kπ﹣ ![]() <x<2kπ+
<x<2kπ+ ![]() ,k∈Z,
,k∈Z,
所以函数的定义域为: ![]()
(2)解:首先, ![]() ,
,
∵ ![]() ,∴﹣3≤log2x≤1,∴函数f(x)的值域为[0,4],
,∴﹣3≤log2x≤1,∴函数f(x)的值域为[0,4],
其次,由题意知:[0,4]{y|y=x2﹣ax+1(﹣1≤x≤2)},且对任意y∈[0,4],总存在唯一x0∈[﹣1,2],使得y=g(x0).以下分三种情况讨论:
①当 ![]() 时,则
时,则 ![]() ,解得a≤﹣2;
,解得a≤﹣2;
②当 ![]() 时,则
时,则 ![]() ,解得a≥4;
,解得a≥4;
③当 ![]() 时,则
时,则 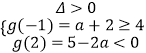 或
或 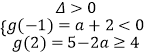 ,解得
,解得 ![]() ;
;
综上: ![]()
【解析】(1)要使原函数有意义,须使 ![]() ,解出即可;(2)先求出函数f(x)在[
,解出即可;(2)先求出函数f(x)在[ ![]() ,2]上的值域,由题意该值域为函数g(x)在[﹣1,2]上值域的子集,按g(x)图象的对称轴在[﹣1,2]的左侧、右侧、内部三种情况进行讨论,结合图象可得端点处函数值g(﹣1)、g(2)的限制条件,得不等式组,分别解出,最后求并集即可;
,2]上的值域,由题意该值域为函数g(x)在[﹣1,2]上值域的子集,按g(x)图象的对称轴在[﹣1,2]的左侧、右侧、内部三种情况进行讨论,结合图象可得端点处函数值g(﹣1)、g(2)的限制条件,得不等式组,分别解出,最后求并集即可;
【考点精析】根据题目的已知条件,利用函数的定义域及其求法和复合函数单调性的判断方法的相关知识可以得到问题的答案,需要掌握求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;复合函数f[g(x)]的单调性与构成它的函数u=g(x),y=f(u)的单调性密切相关,其规律:“同增异减”.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;复合函数f[g(x)]的单调性与构成它的函数u=g(x),y=f(u)的单调性密切相关,其规律:“同增异减”.

【题目】某学校高三年级有学生500人,其中男生300人,女生200人,为了研究学生的数学成绩是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们期中考试的数学分数,然后按性别分为男、女两组,再将两组学生的分数分成5组:[100,110),[110,120),[120,130),[130,140),[140,150]分别加以统计,得到如图所示的频率分布直方图.
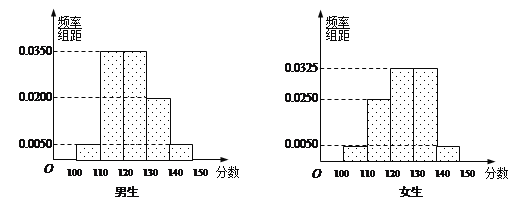
(1)从样本中分数小于110分的学生中随机抽取2人,求两人恰好为一男一女的概率;
(2)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
附:
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
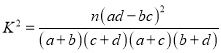 ,
,